Question

【題目】已知函數f（x）=ax3+bx2﹣3x（a，b∈R）在點（1，f（1））處的切線方程為y+2=0．
（1）求函數f（x）的解析式；
（2）若對于區間[﹣2，2]上任意兩個自變量的值x1 ， x2都有|f（x1）﹣f（x2）|≤c，求實數c的最小值；
（3）若過點M（2，m）（m≠2）可作曲線y=f（x）的三條切線，求實數m的取值范圍．

Answer 1

【答案】
（1）解：f'（x）=3ax2+2bx﹣3．

根據題意，得 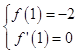即 解得

所以f（x）=x3﹣3x

（2）解：令f'（x）=0，即3x2﹣3=0．得x=±1．

當x∈（﹣∞，﹣1）時，f′（x）＞0，函數f（x）在此區間單調遞增；

當x∈（﹣1，1）時，f′（x）＜0，函數f（x）在此區間單調遞減

因為f（﹣1）=2，f（1）=﹣2，

所以當x∈[﹣2，2]時，f（x）max=2，f（x）min=﹣2．

則對于區間[﹣2，2]上任意兩個自變量的值x1，x2，都有|f（x1）﹣f（x2）|≤|f（x）max﹣f（x）min|=4，所以c≥4．

所以c的最小值為4

（3）解：因為點M（2，m）（m≠2）不在曲線y=f（x）上，所以可設切點為（x0，y0）．

則y0=x03﹣3x0．

因為f'（x0）=3x02﹣3，所以切線的斜率為3x02﹣3．

則3x02﹣3= ，

即2x03﹣6x02+6+m=0．

因為過點M（2，m）（m≠2）可作曲線y=f（x）的三條切線，

所以方程2x03﹣6x02+6+m=0有三個不同的實數解．

所以函數g（x）=2x3﹣6x2+6+m有三個不同的零點．

則g'（x）=6x2﹣12x．令g'（x）=0，則x=0或x=2．

當x∈（﹣∞，0）時，g′（x）＞0，函數g（x）在此區間單調遞增；當x∈（0，2）時，g′（x）＜0，函數g（x）在此區間單調遞減；

所以，函數g（x）在x=0處取極大值，在x=2處取極小值，有方程與函數的關系知要滿足題意必須滿足：

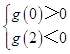，即 ，解得﹣6＜m＜2

【解析】（1）由題意，利用導函數的幾何含義及切點的實質建立a，b的方程，然后求解即可；（2）由題意，對于定義域內任意自變量都使得|f（x1）﹣f（x2）|≤c，可以轉化為求函數在定義域下的最值即可得解；（3）由題意，若過點M（2，m）（m≠2）可作曲線y=f（x）的三條切線，等價與函數在切點處導函數值等于切線的斜率這一方程有3解．
【考點精析】通過靈活運用函數的極值與導數，掌握求函數的極值的方法是:（1）如果在附近的左側,右側,那么是極大值（2）如果在附近的左側,右側,那么是極小值即可以解答此題．