【題目】已知函數
．
（1）若
，求
的單調區間；
（2）證明：（i）
；
（ii）對任意
，
對
恒成立．
【答案】（1）
的單調遞增區間為
，
，的單調遞減區間為
. （2）（i）證明見解析（ii）證明見解析
【解析】
（1）將
代入函數解析式，并求得導函數，由導函數的符號即可判斷的單調區間；
（2）（i）構造函數
并求得
，利用
的單調性求得最大值，即可證明不等式成立.；（ii）由（i）可知將不等式變形可得
成立，構造函數
，因式分解后解一元二次不等式即可證明
對
恒成立．
（1）若，
（
），
令
，得
或
， 則的單調遞增區間為，.
令
，得
，則的單調遞減區間為.
（2）證明：（i）設，
則
（），
令
，得
；
令
，得
.
故
，
從而
，即
.
（ii）函數
由（i）可知
即
，所以
，當
時取等號；
所以當時，則
若
，令
則
，
當時，
.
則當時，，
故對任意，對恒成立.
科目：高中數學 來源： 題型：
【題目】“搜索指數”是網民通過搜索引擎，以每天搜索關鍵詞的次數為基礎所得到的統計指標.“搜索指數”越大，表示網民對該關鍵詞的搜索次數越多，對該關鍵詞相關的信息關注度也越高.下圖是2017年9月到2018年2月這半年中，某個關鍵詞的搜索指數變化的走勢圖.
根據該走勢圖，下列結論正確的是（ ）
A. 這半年中，網民對該關鍵詞相關的信息關注度呈周期性變化
B. 這半年中，網民對該關鍵詞相關的信息關注度不斷減弱
C. 從網民對該關鍵詞的搜索指數來看，去年10月份的方差小于11月份的方差
D. 從網民對該關鍵詞的搜索指數來看，去年12月份的平均值大于今年1月份的平均值
查看答案和解析>>
科目：高中數學 來源： 題型：
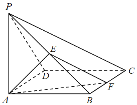
【題目】如圖，在四棱錐
中，底面
為正方形，
底面，
，
為線段
的中點，
為線段
上的動點．
（1）求證：平面
平面
．
（2）試確定點的位置，使平面
與平面
所成的銳二面角為
．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】皮埃爾·德·費馬，法國律師和業余數學家，被譽為“業余數學家之王”，對數學界做出了重大貢獻，其中在1636年發現了：若
是質數，且
互質，那么
的
次方除以的余數恒等于1，后來人們稱該定理為費馬小定理.依此定理若在數集
中任取兩個數，其中一個作為，另一個作為，則所取兩個數不符合費馬小定理的概率為（ ）
A.
B.
C.
D.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在正四棱錐
中，已知異面直線
與
所成的角為
，給出下面三個命題:
:若
，則此四棱錐的側面積為
；
：若
分別為
的中點，則
平面
；
:若
都在球
的表面上，則球
的表面積是四邊形
面積的
倍.
在下列命題中，為真命題的是（ ）
A. 
B. 
C. 
D. 
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某校高一年級開設了豐富多彩的校本課程，現從甲、乙兩個班隨機抽取了5名學生校本課程的學分，統計如下表．
甲 | 8 | 11 | 14 | 15 | 22 |
乙 | 6 | 7 | 10 | 23 | 24 |
用
分別表示甲、乙兩班抽取的5名學生學分的方差，計算兩個班學分的方差．得
______，并由此可判斷成績更穩定的班級是______班．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在直角坐標系.xOy中，曲線C1的參數方程為
（
為參數），以原點O為極點，x軸的正半軸為極軸建立極坐標系，曲線C2的極坐標方程為ρ=4sinθ.
（1）求曲線C1的普通方程和C2的直角坐標方程；
（2）已知曲線C2的極坐標方程為
，點A是曲線C3與C1的交點，點B是曲線C3與C2的交點，且A，B均異于原點O，且|AB|=4
，求α的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
