設
,函數
的定義域為
,且
,當
,有
；函數
是定義在
上單調遞增的奇函數.
(Ⅰ)求
和
的值(用
表示);
(Ⅱ)求的值;
(Ⅲ)當
時, 
對所有的
均成立,求實數
的取值范圍.
(Ⅰ) 
(Ⅱ) 
(Ⅲ)
解(Ⅰ) 因為當,有
所以,令
-----------2分
所以,令
---------4分
(Ⅱ) 令
令
------6分
所以
或
或
----------8分
(Ⅲ)
因為是定義在上單調遞增的奇函數,所以
--------9分
令
----------10分
原題等價于“對于任意
，
恒成立” -------10分
令函數
所以對稱軸
①當
時，只需滿足
（舍去）------11分
②當
時，只需滿足----------12分
，以
③當
時，只需滿足
所以
---13分
綜上所述：--------------14分
（本題(Ⅲ)還可以用分離變量法或數形結合，其它方法酌情給分）
天天向上一本好卷系列答案
小學生10分鐘應用題系列答案科目：高中數學 來源： 題型：
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 5 |
查看答案和解析>>
科目：高中數學 來源： 題型：
（本小題滿分12分）設函數
的定義域為
，當
時，
，且對于任意的實數
、
，都有
．（1）求
；（2）試判斷函數在
上是否存在最小值，若存在，求該最小值；若不存在，說明理由；（3）設數列
各項都是正數，且滿足
，
（
），又設
，
，
， 當
時，試比較
與
的大小，并說明理由．
查看答案和解析>>
科目：高中數學 來源：2012-2013學年吉林省吉林市高三上學期期末考試理科數學試卷（解析版） 題型：選擇題
設函數
的定義域為D，若存在非零實數
使得對于任意
，有
，且
，則稱為M上的高調函數.
現給出下列命題：
① 函數
為R上的1高調函數；
② 函數
為R上的
高調函數；
③ 如果定義域為
的函數
為上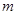
高調函數，那么實數 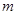的取值范圍是
；
④ 函數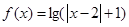
為
上的2高調函數。
其中真命題的個數為
A．0 B．1 C．2 D．3
查看答案和解析>>
科目：高中數學 來源：2010-2011學年福建省高考模擬試題（1） 題型：選擇題
設函數
的定義域為R+，若對于給定的正數
，定義函數
則當函數
,
時，
的值為（ ）
A．
B．
C．
D．
查看答案和解析>>
科目：高中數學 來源：北京市宣武區2010年高三第一次質量檢測數學（理）試題 題型：選擇題
設函數
的定義域為R+，若對于給定的正數K，定義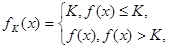函數
，則當函數
時，定積分
的值為
（ ）
A．2ln2+2 B．2ln2-1 C．2ln2 D．2ln2+1
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com