
【題目】已知數列![]() 中,
中, ![]() ,且
,且![]() 對任意正整數
對任意正整數![]() 都成立,數列
都成立,數列![]() 的前
的前![]() 項和為
項和為![]() .
.
(1)若![]() ,且
,且![]() ,求
,求![]() ;
;
(2)是否存在實數![]() ,使數列
,使數列![]() 是公比為1的等比數列,且任意相鄰三項
是公比為1的等比數列,且任意相鄰三項![]() 按某順序排列后成等差數列,若存在,求出所有
按某順序排列后成等差數列,若存在,求出所有![]() 的值;若不存在,請說明理由;
的值;若不存在,請說明理由;
(3)若![]() ,求
,求![]() .(用
.(用![]() 表示).
表示).
【答案】(1) ![]() ;(2)
;(2) ![]() ;(3)
;(3) 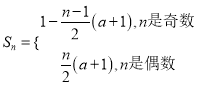 .
.
【解析】試題分析:
(1)由題意求得首項![]() ,公差
,公差![]() ,結合等差數列前n項和公式列方程可得
,結合等差數列前n項和公式列方程可得![]() ;
;
(2)假設存在滿足題意的實數k,分類討論可得![]() ;
;
(3)結合題意分類討論,然后分組求和可得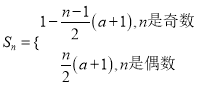 .
.
試題解析:
(1)![]() 時,
時, ![]() ,
,
所以數列![]() 是等差數列,
是等差數列,
此時首項![]() ,公差
,公差![]() ,
,
數列![]() 的前
的前![]() 項和是
項和是![]() ;
;
故![]() ,得
,得![]() ;
;
(2)設數列![]() 是等比數列,則它的公比
是等比數列,則它的公比![]() ,所以
,所以![]() ,
,
①![]() 為等差中項,則
為等差中項,則![]() ,
,
即![]() ,解得
,解得![]() ,不合題意;
,不合題意;
②![]() 為等差中項,則
為等差中項,則![]() ,
,
即![]() ,化簡得:
,化簡得: ![]() ,解得
,解得![]() 或
或![]() (舍去);
(舍去);
③若![]() 為等差中項,則
為等差中項,則![]() ,
,
即![]() ,化簡得:
,化簡得: ![]() ,解得
,解得![]() ;
;
![]() ;
;
綜上可得,滿足要求的實數![]() 有且僅有一個,
有且僅有一個, ![]() ;
;
(3)![]() ,則
,則![]() ,
,
![]() ,
,
當![]() 是偶數時,
是偶數時, ![]()
![]() ,
,
當![]() 是奇數時,
是奇數時, ![]()
![]() ,
,
![]() 也適合上式,
也適合上式,
綜上可得, 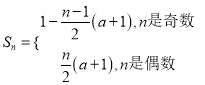 .
.


 特高級教師點撥系列答案
特高級教師點撥系列答案科目:高中數學 來源: 題型:
【題目】在直角坐標系中,曲線![]() 的參數方程為
的參數方程為![]() (
(![]() 為參數),以原點為極點,
為參數),以原點為極點, ![]() 軸的正半軸為極軸,建立極坐標系,曲線
軸的正半軸為極軸,建立極坐標系,曲線![]() 的極坐標方程為
的極坐標方程為![]() .
.
![]() 寫出曲線
寫出曲線![]() 的極坐標的方程以及曲線
的極坐標的方程以及曲線![]() 的直角坐標方程;
的直角坐標方程;
![]() 若過點
若過點![]() (極坐標)且傾斜角為
(極坐標)且傾斜角為![]() 的直線
的直線![]() 與曲線
與曲線![]() 交于
交于![]() ,
, ![]() 兩點,弦
兩點,弦![]() 的中點為
的中點為![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
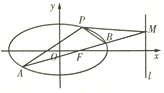
【題目】如圖,橢圓![]() 經過點
經過點![]() ,離心率
,離心率![]() ,直線
,直線![]() 的方程為
的方程為![]() .
.
![]() 求橢圓
求橢圓![]() 的方程;
的方程;
![]()
![]() 是經過右焦點
是經過右焦點![]() 的任一弦(不經過點
的任一弦(不經過點![]() ),設直線
),設直線![]() 與直線
與直線![]() 相交于點
相交于點![]() ,記
,記![]() ,
, ![]() ,
, ![]() 的斜率為
的斜率為![]() ,
, ![]() ,
, ![]() .問:是否存在常數
.問:是否存在常數![]() ,使得
,使得![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,說明理由.
的值;若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在正方體ABCD﹣A1B1C1D1中,M,N,P分別是B1B,B1C1 , CD的中點,則MN與D1P所成角的余弦值為( ) 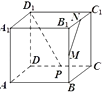
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】①一個命題的逆命題為真,它的否命題也一定為真;
②在△ABC中,“∠B=60°”是“∠A,∠B,∠C三個角成等差數列”的充要條件.
③ ![]() 是
是 ![]() 的充要條件;
的充要條件;
④“am2<bm2”是“a<b”的充分必要條件.
以上說法中,判斷錯誤的有 .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知某食品廠需要定期購買食品配料,該廠每天需要食品配料200千克,配料的價格為1.8元/千克,每次購買配料需支付運費236元,每次購買來的配料還需支付保管費用,其標準如下:7天以內(含7天),無論重量多少,均按10元/天支付;超出7天以外的天數,根據實際剩余配料的重量,以每天0.03元/千克支付.
(1)當9天購買一次配料時,求該廠用于配料的保管費用![]() 是多少元?
是多少元?
(2)設該廠![]() 天購買一次配料,求該廠在這
天購買一次配料,求該廠在這![]() 天中用于配料的總費用
天中用于配料的總費用![]() (元)關于
(元)關于![]() 的函數關系式,并求該廠多少天購買一次配料才能使平均每天支付的費用最少?
的函數關系式,并求該廠多少天購買一次配料才能使平均每天支付的費用最少?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com