
極坐標(biāo)系與直角坐標(biāo)系 有相同的長度單位,以原點
有相同的長度單位,以原點 為極點,以
為極點,以 軸正半軸為極軸.已知直線
軸正半軸為極軸.已知直線 的參數(shù)方程為
的參數(shù)方程為 (
( 為參數(shù)),曲線
為參數(shù)),曲線 的極坐標(biāo)方程為
的極坐標(biāo)方程為 .
.
(Ⅰ)求 的直角坐標(biāo)方程;
的直角坐標(biāo)方程;
(Ⅱ)設(shè)直線 與曲線
與曲線 交于
交于 兩點,求弦長
兩點,求弦長 .
.
 教材全解字詞句篇系列答案
教材全解字詞句篇系列答案科目:高中數(shù)學(xué) 來源: 題型:解答題
(本小題滿分10分)選修4—4,坐標(biāo)系與參數(shù)方程
已知曲線 ,直線
,直線 :
: (
( 為參數(shù)).
為參數(shù)).
(I)寫出曲線 的參數(shù)方程,直線
的參數(shù)方程,直線 的普通方程;
的普通方程;
(II)過曲線 上任意一點
上任意一點 作與
作與 夾角為
夾角為 的直線,交
的直線,交 于點
于點 ,
, 的最大值與最小值.
的最大值與最小值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
已知在直角坐標(biāo)系xOy中,曲線C的參數(shù)方程為 (
( 為參數(shù)),直線
為參數(shù)),直線 經(jīng)過定點P(3,5),傾斜角為
經(jīng)過定點P(3,5),傾斜角為 (1)寫出直線
(1)寫出直線 的參數(shù)方程和曲線C的標(biāo)準(zhǔn)方程;(2)設(shè)直線
的參數(shù)方程和曲線C的標(biāo)準(zhǔn)方程;(2)設(shè)直線 與曲線C相交于A、B兩點,求
與曲線C相交于A、B兩點,求 的值
的值
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
在直角坐標(biāo)系 中,曲線
中,曲線 的參數(shù)方程為
的參數(shù)方程為 (
( 為參數(shù)),若以直角坐標(biāo)系的原點
為參數(shù)),若以直角坐標(biāo)系的原點 為極點,
為極點, 軸的正半軸為極軸建立極坐標(biāo),曲線
軸的正半軸為極軸建立極坐標(biāo),曲線 的極坐標(biāo)方程為
的極坐標(biāo)方程為 (其中
(其中 為常數(shù)).
為常數(shù)).
(1)若曲線 與曲線
與曲線 只有一個公共點,求
只有一個公共點,求 的取值范圍;
的取值范圍;
(2)當(dāng) 時,求曲線
時,求曲線 上的點與曲線
上的點與曲線 上的點的最小距離.
上的點的最小距離.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
已知曲線 的參數(shù)方程為
的參數(shù)方程為
 是參數(shù)
是參數(shù) ,
, 是曲線
是曲線 與
與 軸正半軸的交點.以坐標(biāo)原點
軸正半軸的交點.以坐標(biāo)原點 為極點,
為極點, 軸正半軸為極軸建立極坐標(biāo)系,求經(jīng)過點
軸正半軸為極軸建立極坐標(biāo)系,求經(jīng)過點 與曲線
與曲線 只有一個公共點的直線
只有一個公共點的直線 的極坐標(biāo)方程.
的極坐標(biāo)方程.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
已知曲線 的極坐標(biāo)方程為
的極坐標(biāo)方程為 ,以極點為原點,極軸為軸的正半軸建立直角坐標(biāo)系,直線
,以極點為原點,極軸為軸的正半軸建立直角坐標(biāo)系,直線 的參數(shù)方程
的參數(shù)方程
(Ⅰ)寫出直線 的普通方程與曲線
的普通方程與曲線 的直角坐標(biāo)方程;
的直角坐標(biāo)方程;
(Ⅱ)設(shè)曲線 經(jīng)過伸縮變換
經(jīng)過伸縮變換 得到曲線
得到曲線 ,在曲線
,在曲線 上求一點
上求一點 ,使點
,使點 到直線
到直線 的距離最小,并求出最小距離.
的距離最小,并求出最小距離.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
已知圓 的參數(shù)方程為
的參數(shù)方程為 (
( 為參數(shù)),以坐標(biāo)原點
為參數(shù)),以坐標(biāo)原點 為極點,x軸的正半軸為極軸建立極坐標(biāo)系,圓
為極點,x軸的正半軸為極軸建立極坐標(biāo)系,圓 的極坐標(biāo)方程為
的極坐標(biāo)方程為 .
.
(Ⅰ)將圓 的參數(shù)方程化為普通方程,將圓
的參數(shù)方程化為普通方程,將圓 的極坐標(biāo)方程化為直角坐標(biāo)方程;
的極坐標(biāo)方程化為直角坐標(biāo)方程;
(Ⅱ)圓 、
、 是否相交,若相交,請求出公共弦的長;若不相交,請說明理由.
是否相交,若相交,請求出公共弦的長;若不相交,請說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
[選修4 - 4:坐標(biāo)系與參數(shù)方程](本小題滿分10分)
在直角坐標(biāo)系 中,直線
中,直線 的參數(shù)方程為
的參數(shù)方程為 (
( 為參數(shù)),若以直角坐標(biāo)系
為參數(shù)),若以直角坐標(biāo)系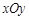 的
的 點為極點,
點為極點,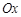 為極軸,且長度單位相同,建立極坐標(biāo)系,得曲線
為極軸,且長度單位相同,建立極坐標(biāo)系,得曲線 的極坐標(biāo)方程為
的極坐標(biāo)方程為 .直線
.直線 與曲線
與曲線 交于
交于 兩點,求
兩點,求 .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:單選題
右表提供了某廠節(jié)能降耗技術(shù)改造后生產(chǎn)A產(chǎn)品過程中記錄的產(chǎn)量x(噸)與相應(yīng)的生產(chǎn)能耗y(噸標(biāo)準(zhǔn)煤)的幾組對應(yīng)數(shù)據(jù).根據(jù)下表提供的數(shù)據(jù),求出y關(guān)于x的線性回歸方程為 =0.7x+0.35,那么表中t的值為( )
=0.7x+0.35,那么表中t的值為( )
| x | 3 | 4 | 5 | 6 |
| y | 2.5 | t | 4 | 4.5 |
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com