
| Sn |
| n |
| 1 |
| 2 |
| an |
| an+2011 |
| n |
| n+2011 |
| k(q+2011) |
| q-k |
| Sn |
| n |
| 3n+1 |
| 2n-1 |
| 3n+1 |
| 2n-1 |
| 3n+2+1 |
| 2n+3 |
| 3n+1 |
| 2n-1 |
| -4(4n-3)3n+4 |
| (2n-1)(2n+3) |
| 3n-1 |
| 2n-1 |
| 3n-1 |
| 2n-1 |
| 3n+2-1 |
| 2n+3 |
| 3n-1 |
| 2n-1 |
| 4(4n-3)3n+4 |
| (2n-1)(2n+3) |
| 8 |
| 3 |
| 8 |
| 3 |
| 8 |
| 3 |
| n |
| n+2011 |
| k |
| k+2011 |
| p |
| p+2011 |
| q |
| q+2011 |
| k(q+2011) |
| q-k |


科目:高中數學 來源: 題型:
| 1 |
| 2 |
| an |
| an+2012 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
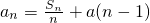 .
.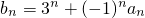 ,且數列{bn}是單調遞增數列,求實數a的取值范圍;
,且數列{bn}是單調遞增數列,求實數a的取值范圍; ,數列{cn}滿足:
,數列{cn}滿足: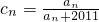 ,對于任意給定的正整數k,是否存在p,q∈N*,使ck=cp•cq?若存在,求p,q的值(只要寫出一組即可);若不存在,說明理由.
,對于任意給定的正整數k,是否存在p,q∈N*,使ck=cp•cq?若存在,求p,q的值(只要寫出一組即可);若不存在,說明理由.查看答案和解析>>
科目:高中數學 來源:2012-2013學年江蘇省宿遷市泗陽縣致遠中學高一(上)第一次教學質量檢測數學試卷(奧數班)(解析版) 題型:解答題
 .
. 對任意的正整數n恒成立,求實數a的取值范圍;
對任意的正整數n恒成立,求實數a的取值范圍; ,數列{cn}滿足:
,數列{cn}滿足: ,對于任意給定的正整數k,是否存在p,q∈N*,使得ck=cp•cq?若存在,求出p,q的值(只要寫出一組即可);若不存在說明理由.
,對于任意給定的正整數k,是否存在p,q∈N*,使得ck=cp•cq?若存在,求出p,q的值(只要寫出一組即可);若不存在說明理由.查看答案和解析>>
科目:高中數學 來源:2011-2012學年江蘇省徐州市邳州市運河中學高三(上)12月學情調研數學試卷(1)(解析版) 題型:解答題
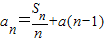 .
. ,且數列{bn}是單調遞增數列,求實數a的取值范圍;
,且數列{bn}是單調遞增數列,求實數a的取值范圍;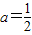 ,數列{cn}滿足:
,數列{cn}滿足: ,對于任意給定的正整數k,是否存在p,q∈N*,使ck=cp•cq?若存在,求p,q的值(只要寫出一組即可);若不存在,說明理由.
,對于任意給定的正整數k,是否存在p,q∈N*,使ck=cp•cq?若存在,求p,q的值(只要寫出一組即可);若不存在,說明理由.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com