
(08年蕪湖一中理)若存在實(shí)常數(shù)![]() 和
和![]() ,使得函數(shù)
,使得函數(shù)![]() 和
和![]() 對其定義域上的任意實(shí)數(shù)
對其定義域上的任意實(shí)數(shù)![]() 分別滿足:
分別滿足:![]() 和
和![]() ,則稱直線
,則稱直線![]()
![]() 為
為![]() 和
和![]() 的“隔離直線”.已知
的“隔離直線”.已知![]() ,
,![]() (其中
(其中![]() 為自然對數(shù)的底數(shù)).
為自然對數(shù)的底數(shù)).
(1)求![]() 的極值;
的極值;
(2) 函數(shù)![]() 和
和![]() 是否存在隔離直線?若存在,求出此隔離直線方程;若不存在,請說明理由.
是否存在隔離直線?若存在,求出此隔離直線方程;若不存在,請說明理由.
解:(1) ![]()
![]() ,
, ![]() .
.
當(dāng)![]() 時(shí),
時(shí),![]() .
.
![]() 當(dāng)
當(dāng)![]() 時(shí),
時(shí),![]() ,此時(shí)函數(shù)
,此時(shí)函數(shù)![]() 遞減;
遞減;
當(dāng)![]() 時(shí),
時(shí),![]() ,此時(shí)函數(shù)
,此時(shí)函數(shù)![]() 遞增;
遞增;
∴當(dāng)![]() 時(shí),
時(shí),![]() 取極小值,其極小值為
取極小值,其極小值為![]() .…………6分
.…………6分
(2)解法一:由(1)可知函數(shù)![]() 和
和![]() 的圖象在
的圖象在![]() 處有公共點(diǎn),
處有公共點(diǎn),
因此若存在![]() 和
和![]() 的隔離直線,則該直線過這個公共點(diǎn).
的隔離直線,則該直線過這個公共點(diǎn).
設(shè)隔離直線的斜率為![]() ,則直線方程為
,則直線方程為![]() ,即
,即![]() .
.
由![]() ,可得
,可得![]() 當(dāng)
當(dāng)![]() 時(shí)恒成立
時(shí)恒成立
![]() ,
, ![]() 由
由![]() ,得
,得![]() .
.
下面證明![]() 當(dāng)
當(dāng)![]() 時(shí)恒成立.令
時(shí)恒成立.令![]()
![]() ,
,
則![]() ,
,
當(dāng)![]() 時(shí),
時(shí),![]() .
.
![]() 當(dāng)
當(dāng)![]() 時(shí),
時(shí),![]() ,此時(shí)函數(shù)
,此時(shí)函數(shù)![]() 遞增;
遞增;
當(dāng)![]() 時(shí),
時(shí),![]() ,此時(shí)函數(shù)
,此時(shí)函數(shù)![]() 遞減;
遞減;
∴當(dāng)![]() 時(shí),
時(shí),![]() 取極大值,其極大值為
取極大值,其極大值為![]() .
.
從而![]() ,即
,即![]() 恒成立.
恒成立.
∴函數(shù)![]() 和
和![]() 存在唯一的隔離直線
存在唯一的隔離直線![]() .…………………12分
.…………………12分
解法二: 由(1)可知當(dāng)![]() 時(shí),
時(shí),![]() (當(dāng)且當(dāng)
(當(dāng)且當(dāng)![]() 時(shí)取等號) .
時(shí)取等號) .
若存在![]() 和
和![]() 的隔離直線,則存在實(shí)常數(shù)
的隔離直線,則存在實(shí)常數(shù)![]() 和
和![]() ,使得
,使得![]() 和
和![]() 恒成立,
恒成立,
令![]() ,則
,則![]() 且
且![]()


 云南師大附小一線名師提優(yōu)作業(yè)系列答案
云南師大附小一線名師提優(yōu)作業(yè)系列答案 沖刺100分單元優(yōu)化練考卷系列答案
沖刺100分單元優(yōu)化練考卷系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
(08年蕪湖一中理) 已知數(shù)列{an},Sn是其前n項(xiàng)和,且![]() ,(1)求數(shù)列{an}的通項(xiàng)公式;(2)設(shè)
,(1)求數(shù)列{an}的通項(xiàng)公式;(2)設(shè)![]() 是數(shù)列{bn}的前n項(xiàng)和,求使得
是數(shù)列{bn}的前n項(xiàng)和,求使得![]() 對所有
對所有![]() 都成立的最小正整數(shù)m.
都成立的最小正整數(shù)m.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
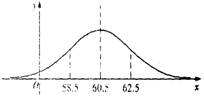
(08年蕪湖一中理)某單位1 000名青年職員的體重x ( kg )服從正態(tài)分布N (![]() , 22 ),且正態(tài)分布的密度曲線如圖所示,若58.5 ~ 62.5 kg體重屬于正常情況,則這1 000名青年職員中體重屬于正常情況的人數(shù)約是(其中
, 22 ),且正態(tài)分布的密度曲線如圖所示,若58.5 ~ 62.5 kg體重屬于正常情況,則這1 000名青年職員中體重屬于正常情況的人數(shù)約是(其中![]() (1)≈0.841)( )
(1)≈0.841)( )
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺 | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com