解:(Ⅰ)根據(jù)題意:易知y=lnx與y=
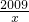
的交點(diǎn)為A(α,
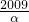
),
y=e
x與y=
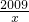
的交點(diǎn)為B(β,
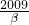
);由K
AB=-1,易知α•β=2009(4分)
(Ⅱ)設(shè)F(x)=

x
2+lnx-

x
3,則F′(x)=x+

-2x
2=
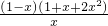
∵x>1,F(xiàn)′(x)<0∴F(x)在區(qū)間(1,+∝)上是減函數(shù)又∵F(1)=-

<0
∴

x
2+lnx-

x
3<0,即

x
2+lnx<

x
3,x∈(1,+∞)
∴在區(qū)間(1,+∞)上,函數(shù)f(x)圖象在函數(shù)g(x)=

x
3圖象的下方(9分)
(Ⅲ)當(dāng)n=1時(shí),左邊=x+

+2,右邊=x+

+2,不等式成立;
當(dāng)n≥2時(shí),[h(x)]
n-h(x
n)=(x+

)
n-(x
n+
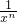
)
=

[C
n1(x
n-2+
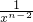
)+C
n2(x
n-4+
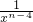
)+…+C
nn-1(
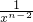
+x
n-2)]
由已知,x>0
∴[h(x)]
n-ln(x
n)≥C
n1+C
n2+…+C
nn-1=2
n-2
∴[h(x)]
n+2≥h(x
n)+2
n.(15分)
分析:(Ⅰ)將“方程xf(x)-

x
3=2009的根”轉(zhuǎn)化為:“函數(shù)y=lnx與y=
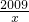
”的交點(diǎn),將“方程xe
x=2009的根”轉(zhuǎn)化為:“函數(shù)y=e
x與y=
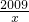
”的交點(diǎn);最由K
AB=-1,求得α•β
(Ⅱ)構(gòu)造“函數(shù)F(x)=

x
2+lnx-

x
3”,將問(wèn)題轉(zhuǎn)化為:“F(x)≤0恒成立”,再用導(dǎo)數(shù)法,研究其單調(diào)性,求得其最大值即可.
(Ⅲ)當(dāng)n=1時(shí),左邊=x+

+2,右邊=x+

+2,不等式成立;當(dāng)n≥2時(shí),由[h(x)]
n-h(x
n)=(x+

)
n-(x
n+
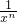
)
=

[C
n1(x
n-2+
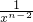
)+C
n2(x
n-4+
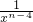
)+…+C
nn-1(
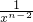
+x
n-2)]作差比較.
點(diǎn)評(píng):本題主要考查函數(shù)與方程的綜合運(yùn)用,主要涉及了方程根的問(wèn)題轉(zhuǎn)化為函數(shù)圖象的交點(diǎn),不等式恒成立問(wèn)題,轉(zhuǎn)化為函數(shù)的最值問(wèn)題,比較法證明不等式等.

 x2+lnx.
x2+lnx. x3=2009的根,β是方程xex=2009的根,求α•β的值.
x3=2009的根,β是方程xex=2009的根,求α•β的值. x3圖象的下方;
x3圖象的下方;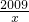 的交點(diǎn)為A(α,
的交點(diǎn)為A(α,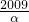 ),
),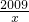 的交點(diǎn)為B(β,
的交點(diǎn)為B(β,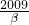 );由KAB=-1,易知α•β=2009(4分)
);由KAB=-1,易知α•β=2009(4分) x2+lnx-
x2+lnx- x3,則F′(x)=x+
x3,則F′(x)=x+ -2x2=
-2x2=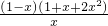
 <0
<0 x2+lnx-
x2+lnx- x3<0,即
x3<0,即 x2+lnx<
x2+lnx< x3,x∈(1,+∞)
x3,x∈(1,+∞) x3圖象的下方(9分)
x3圖象的下方(9分) +2,右邊=x+
+2,右邊=x+ +2,不等式成立;
+2,不等式成立; )n-(xn+
)n-(xn+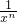 )
) [Cn1(xn-2+
[Cn1(xn-2+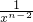 )+Cn2(xn-4+
)+Cn2(xn-4+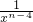 )+…+Cnn-1(
)+…+Cnn-1(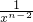 +xn-2)]
+xn-2)] x3=2009的根”轉(zhuǎn)化為:“函數(shù)y=lnx與y=
x3=2009的根”轉(zhuǎn)化為:“函數(shù)y=lnx與y=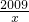 ”的交點(diǎn),將“方程xex=2009的根”轉(zhuǎn)化為:“函數(shù)y=ex與y=
”的交點(diǎn),將“方程xex=2009的根”轉(zhuǎn)化為:“函數(shù)y=ex與y=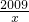 ”的交點(diǎn);最由KAB=-1,求得α•β
”的交點(diǎn);最由KAB=-1,求得α•β x2+lnx-
x2+lnx- x3”,將問(wèn)題轉(zhuǎn)化為:“F(x)≤0恒成立”,再用導(dǎo)數(shù)法,研究其單調(diào)性,求得其最大值即可.
x3”,將問(wèn)題轉(zhuǎn)化為:“F(x)≤0恒成立”,再用導(dǎo)數(shù)法,研究其單調(diào)性,求得其最大值即可. +2,右邊=x+
+2,右邊=x+ +2,不等式成立;當(dāng)n≥2時(shí),由[h(x)]n-h(xn)=(x+
+2,不等式成立;當(dāng)n≥2時(shí),由[h(x)]n-h(xn)=(x+ )n-(xn+
)n-(xn+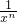 )
) [Cn1(xn-2+
[Cn1(xn-2+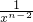 )+Cn2(xn-4+
)+Cn2(xn-4+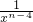 )+…+Cnn-1(
)+…+Cnn-1(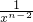 +xn-2)]作差比較.
+xn-2)]作差比較.


 已知函數(shù)f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函數(shù)f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<