【題目】采用系統(tǒng)抽樣方法從960人中抽取32人做問卷調(diào)查，為此將他們隨即編號為1，2…960，分組后在第一組采用簡單隨機抽樣的方法抽到的號碼為5，抽到的32人中，編號落入?yún)^(qū)間[1，450]的人做問卷A，編號落入?yún)^(qū)間[451，750]的人做問卷B，其余的人做問卷C，則抽到的32人中，做問卷C的人數(shù)為（ ）
A.15
B.10
C.9
D.7
【答案】D
【解析】解：∵960÷32=30，∴由題意可得抽到的號碼構(gòu)成以5為首項、以30為公差的等差數(shù)列，
且此等差數(shù)列的通項公式為an=5+（n﹣1）30=30n﹣25．
落人區(qū)間[751，960]的人做問卷C，
由 751≤30n﹣25≤960，
即776≤30n≤985
解得25 
≤n≤32 
．
再由n為正整數(shù)可得26≤n≤32，
∴做問卷C的人數(shù)為32﹣26+1=7，
故選：D．
由題意可得抽到的號碼構(gòu)成以5為首項、以30為公差的等差數(shù)列，求得此等差數(shù)列的通項公式為an=5+（n﹣1）30=30n﹣25，由751≤30n﹣25≤981求得正整數(shù)n的個數(shù)，即為所求．
科目：高中數(shù)學(xué) 來源： 題型：
【題目】已知二次函數(shù)f（x）=ax2+（2b﹣1）x+6b﹣a為偶函數(shù)，且f（x+1）﹣f（x）=2x+1．
（1）求函數(shù)f（x）的解析式；
（2）設(shè)g（x）=f（x）+λx，求函數(shù)g（x）在[0，1]內(nèi)的最小值．
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】各項為正數(shù)的數(shù)列{an}的前n項和為Sn ， 且滿足：Sn= 
an2+ 
an+ （n∈N*）
（1）求an
（2）設(shè)數(shù)列{ 
}的前n項和為Tn ， 證明：對一切正整數(shù)n，都有Tn＜ 
．
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】如圖，四棱錐P﹣ABCD中，底面ABCD為矩形，PA⊥平面ABCD，E為PD的中點．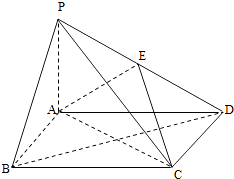 
（1）證明：PB∥平面AEC；
（2）設(shè)AP=1，AD= 
，三棱錐P﹣ABD的體積V= 
，求A到平面PBC的距離．
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】已知
是橢圓
的左、右焦點，
為坐標(biāo)原點，點
在橢圓上，線段
與
軸的交點為
，且
．
（1）求橢圓的標(biāo)準(zhǔn)方程；
（2）圓
是以
為直徑的圓，直線
與圓
相切，并與橢圓交于不同的兩點
，
，當(dāng)
，且滿足
時，求
的面積
的取值范圍．
請考生在第22、23兩題中任選一題作答．注意：只能做所選定的題目.如果多做，則按所做的第一個題目計分．
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】
已知函數(shù)
，
．
（1）若曲線
在點
處的切線與直線
垂直，求
的值；
（2）若
存在極小值
時，不等式
恒成立，求實數(shù)
的取值范圍；
（3）當(dāng)
時，如果存在兩個不相等的正數(shù)
，使得
，求證：
．
請考生在第22、23兩題中任選一題作答．注意：只能做所選定的題目.如果多做，則按所做的第一個題目計分．
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】
如圖，甲向如圖1所示的平面區(qū)域內(nèi)隨機擲點、乙向如圖2所示的平面區(qū)域內(nèi)隨機擲點，假設(shè)點落在區(qū)域內(nèi)任意一點的可能性相同．已知圖1中小圓的半徑是大圓半徑的二分之一，圖2中小正方形的頂點為大正方形各邊的中點．
（1）甲、乙各擲點一次，求至少有一人擲點落在陰影區(qū)域的概率；
（2）甲、乙各擲點兩次，記點落在陰影區(qū)域的次數(shù)為
，求
的分布列和數(shù)學(xué)期望．
圖1圖2
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】已知函數(shù)
在
處的切線的斜率為1.
（1）如果常數(shù)
，求函數(shù)
在區(qū)間
上的最大值；
（2）對于
，如果方程
在
上有且只有一個解，求
的值.
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】選修4-4：坐標(biāo)系與參數(shù)方程
在直角坐標(biāo)系
中，直線
的參數(shù)方程為
（
為參數(shù)， 
）.以原點
為極點，以
軸正半軸為極軸，與直角坐標(biāo)系
取相同的長度單位，建立極坐標(biāo)系.設(shè)曲線
的極坐標(biāo)方程為
.
（Ⅰ）設(shè)
為曲線
上任意一點，求
的取值范圍；
（Ⅱ）若直線
與曲線
交于兩點
， 
，求
的最小值.
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com