
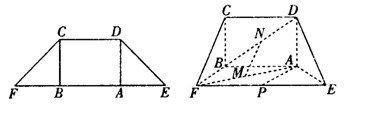
如圖,在等腰梯形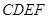 中,
中,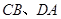 是梯形的高,
是梯形的高,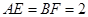 ,
, ,現將梯形沿
,現將梯形沿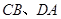 折起,使
折起,使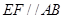 ,且
,且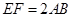 ,得一簡單組合體
,得一簡單組合體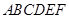 如圖所示,已知
如圖所示,已知 分別為
分別為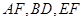 的中點.
的中點.
(1)求證: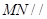 平面
平面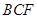 ;
;
(2)求證: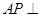 平面
平面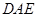 .
.
(1)證明過程詳見解析;(2)證明過程詳見解析.
【解析】
試題分析:本題考查線面平行、線面垂直的證明,考查學生的空間想象能力和推理論證能力.第一問,利用矩形和三角形的性質,先證明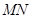 平行于
平行于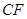 ,利用線面平行的判定定理證明;第二問,注意折起前和折起后的一些性質是不變的,要證明線面垂直,只需證明的是線和平面內的2條相交直線都垂直.
,利用線面平行的判定定理證明;第二問,注意折起前和折起后的一些性質是不變的,要證明線面垂直,只需證明的是線和平面內的2條相交直線都垂直.
試題解析:(1)證明:連結 .∵四邊形
.∵四邊形 是矩形,
是矩形,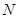 為
為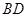 中點,
中點,
∴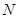 為
為 中點,
中點,
在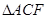 中,
中,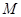 為
為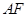 中點,故
中點,故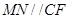 .
.
∵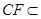 平面
平面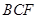 ,
,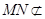 平面
平面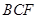 ,∴
,∴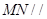 平面
平面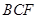 .(5分)
.(5分)
(2)依題意知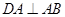 ,
,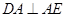 且
且 ,
,
∴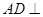 平面
平面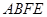 .
.
∵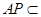 平面
平面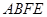 ,∴
,∴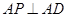 .
.
∵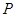 為
為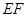 中點,∴
中點,∴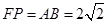 ,
,
結合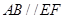 ,知四邊形
,知四邊形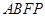 是平行四邊形,
是平行四邊形,
∴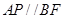 ,
, .
.
而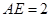 ,
,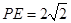 ,∴
,∴ ,∴
,∴ ,即
,即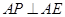 .
.
又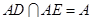 ,∴
,∴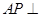 平面
平面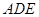 .(12分)
.(12分)
考點:1.線面平行的判定定理;2.線面垂直的判定.


科目:高中數學 來源: 題型:
(12分)如圖,在等腰梯形![]() 中,已知
中,已知![]() 均為梯形的高,且
均為梯形的高,且![]() 。現沿
。現沿![]() 將
將![]() 和
和![]() 折起,使點
折起,使點![]() 重合為一點
重合為一點![]() ,如圖②所示。又點
,如圖②所示。又點![]() 為線段
為線段![]() 的中點,點
的中點,點![]() 在線段
在線段![]() 上,且
上,且![]() 。
。
(1)求線段![]() 的長;
的長;
(2)求二面角![]() 的大小。
的大小。

查看答案和解析>>
科目:高中數學 來源:2013屆廣東省高二上學期期末考試理科數學試卷 題型:選擇題
如圖,在等腰梯形 中,
中, ,且
,且 . 設
. 設 ,
, ,以
,以 ,
, 為焦點且過點
為焦點且過點 的雙曲線的離心率為
的雙曲線的離心率為 ,以
,以 ,
, 為焦點且過點
為焦點且過點 的橢圓的離心率為
的橢圓的離心率為 ,則( )
,則( )

A.隨著角度 的增大,
的增大, 增大,
增大, 為定值
為定值
B.隨著角度 的增大,
的增大, 減小,
減小, 為定值
為定值
C.隨著角度 的增大,
的增大, 增大,
增大, 也增大
也增大
D.隨著角度 的增大,
的增大, 減小,
減小, 也減小
也減小
查看答案和解析>>
科目:高中數學 來源:2010年山西省高一上學期期中考試數學試卷 題型:選擇題
如圖,在等腰梯形 中,
中, ,且
,且 .設
.設 ,以
,以 為焦點且過點
為焦點且過點 的雙曲線的離心率為
的雙曲線的離心率為 ,以
,以 為焦點且過點
為焦點且過點 的橢圓的離心率為
的橢圓的離心率為 ,則
( )
,則
( )
A.隨著角度 的增大,
的增大, 增大,
增大, 為定值
為定值
B.隨著角度 的增大,
的增大, 減小,
減小, 為定值
為定值
C.隨著角度 的增大,
的增大, 增大,
增大, 也增
也增
D.隨著角度 的增大,
的增大, 減小,
減小, 也減小
也減小

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com