【題目】下列命題中：
①若命題
，
，則
，
；
②將
的圖象沿
軸向右平移
個單位，得到的圖象對應函數為
；
③“
”是“
”的充分必要條件；
④已知
為圓
內異于圓心的一點，則直線
與該圓相交.
其中正確的個數是（ ）
A. 4B. 3C. 2D. 1
科目：高中數學 來源： 題型：
【題目】黨的十九大明確把精準脫貧作為決勝全面建成小康社會必須打好的三大攻堅戰之一,為堅決打贏脫貧攻堅戰，某幫扶單位為幫助定點扶貧村扶貧. 此幫扶單位為了了解某地區貧困戶對其所提供的幫扶的滿意度，隨機調查了40個貧困戶，得到貧困戶的滿意度評分如下：
貧困戶編號 | 評分 | 貧困戶編號 | 評分 | 貧困戶編號 | 評分 | 貧困戶編號 | 評分 | |||
1 2 3 4 5 6 7 8 9 10 | 78 73 81 92 95 85 79 84 63 86 | 11 12 13 14 15 16 17 18 19 20 | 88 86 95 76 97 78 88 82 76 89 | 21 22 23 24 25 26 27 28 29 30 | 79 83 72 74 91 66 80 83 74 82 | 31 32 33 34 35 36 37 38 39 40 | 93 78 75 81 84 77 81 76 85 89 |
用系統抽樣法從40名貧困戶中抽取容量為10的樣本，且在第一分段里隨機抽到的評分數據為92.
（1）請你列出抽到的10個樣本的評分數據；
（2）計算所抽到的10個樣本的均值
和方差
；
（3）在（2）條件下，若貧困戶的滿意度評分在
之間，則滿意度等級為“
級”.運用樣本估計總體的思想，現從（1）中抽到的10個樣本的滿意度為“
級”貧困戶中隨機地抽取2戶，求所抽到2戶的滿意度均評分均“超過80”的概率.
（參考數據：
）
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某社區消費者協會為了解本社區居民網購消費情況，隨機抽取了100位居民作為樣本，就最近一年來網購消費金額(單位：千元)，網購次數和支付方式等進行了問卷調査.經統計這100位居民的網購消費金額均在區間
內，按
，
，
，
，
，
分成6組，其頻率分布直方圖如圖所示.
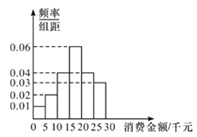
（1）估計該社區居民最近一年來網購消費金額的中位數；
（2）將網購消費金額在20千元以上者稱為“網購迷”，補全下面的
列聯表，并判斷有多大把握認為“網購迷與性別有關系”；
男 | 女 | 合計 | |
網購迷 | 20 | ||
非網購迷 | 45 | ||
合計 | 100 |
（3）調査顯示，甲、乙兩人每次網購采用的支付方式相互獨立，兩人網購時間與次數也互不. 影響.統計最近一年來兩人網購的總次數與支付方式，所得數據如下表所示：
網購總次數 | 支付寶支付次數 | 銀行卡支付次數 | 微信支付次數 | |
甲 | 80 | 40 | 16 | 24 |
乙 | 90 | 60 | 18 | 12 |
將頻率視為概率，若甲、乙兩人在下周內各自網購2次，記兩人采用支付寶支付的次數之和為
，求的數學期望.
附：觀測值公式：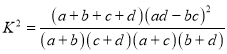
臨界值表：
| 0.01 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知三棱錐P-ABC（如圖1）的展開圖如圖2，其中四邊形ABCD為邊長等于
的正方形，△ABE和△BCF均為正三角形，在三棱錐P-ABC中.
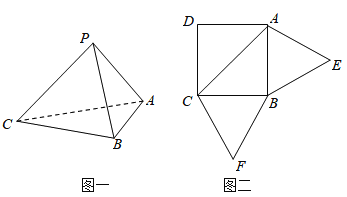
（1）證明：平面PAC⊥平面ABC；
（2）若M，N分別是AP，BC的中點，請判斷三棱錐M-BCP和三棱錐N-APC體積的大小關系并加以證明.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知正四棱錐
的底面邊長和高都為2.現從該棱錐的5個頂點中隨機選取3個點構成三角形，設隨機變量
表示所得三角形的面積.
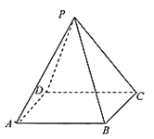
（1）求概率
的值；
（2）求隨機變量的概率分布及其數學期望
.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】甲、乙兩人參加一個射擊的中獎游戲比賽，在相同條件下各打靶50次，統計每次打靶所得環數，得下列頻數分布表．
環數 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
甲的頻數 | 0 | 1 | 4 | 7 | 14 | 16 | 6 | 2 |
乙的頻數 | 1 | 2 | 5 | 6 | 10 | 16 | 8 | 2 |
比賽中規定所得環數為1，2，3，4時獲獎一元，所得環數為5，6，7時獲獎二元，所得環數為8，9時獲獎三元，所得環數為10時獲獎四元，沒命中則無獎．
（1）根據上表，在答題卡給定的坐標系內畫出甲射擊50次獲獎金額（單位：元）的條形圖；
（2）估計甲射擊1次所獲獎至少為三元的概率；
（3）要從甲、乙兩人中選拔一人參加射擊比賽，請你根據甲、乙兩人所獲獎金額的平均數和方差作出選擇．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】過拋物線
的焦點
且斜率為
的直線
與拋物線交于
兩點（
在第一象限），以
為直徑的圓分別與
軸相切于
兩點，則下列結論正確的是（ ）
A.拋物線的焦點坐標為
B.
C.
為拋物線
上的動點，
，則
D.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】為迎接2022年冬奧會，北京市組織中學生開展冰雪運動的培訓活動，并在培訓結束后對學生進行了考核．記
表示學生的考核成績，并規定
為考核優秀．為了了解本次培訓活動的效果，在參加培訓的學生中隨機抽取了30名學生的考核成績，并作成如下莖葉圖：
（Ⅰ）從參加培訓的學生中隨機選取1人，請根據圖中數據，估計這名學生考核優秀的概率；
（Ⅱ）從圖中考核成績滿足
的學生中任取2人，求至少有一人考核優秀的概率；
（Ⅲ）記
表示學生的考核成績在區間
的概率，根據以往培訓數據，規定當
時培訓有效．請根據圖中數據，判斷此次中學生冰雪培訓活動是否有效，并說明理由．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】研究機構對某校學生往返校時間的統計資料表明：該校學生居住地到學校的距離
（單位：千米）和學生花費在上學路上的時間
（單位：分鐘）有如下的統計資料：
到學校的距離 | 1.8 | 2.6 | 3.1 | 4.3 | 5.5 | 6.1 |
花費的時間 | 17.8 | 19.6 | 27.5 | 31.3 | 36.0 | 43.2 |
如果統計資料表明與有線性相關關系，試求：
（1）判斷與是否有很強的線性相關性？
（相關系數
的絕對值大于0.75時，認為兩個變量有很強的線性相關性，精確到0.01）
（2）求線性回歸方程
（精確到0.01）；
（3）將
分鐘的時間數據
稱為美麗數據，現從這6個時間數據中任取2個，求抽取的2個數據全部為美麗數據的概率.
參考數據：
，
，
，
，
，
參考公式：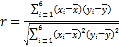
，
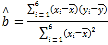
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
