
【題目】已知橢圓![]() :
:![]() 的離心率
的離心率![]() ,左、右焦點分別為
,左、右焦點分別為![]() 、
、![]() ,拋物線
,拋物線![]() 的焦點
的焦點![]() 恰好是該橢圓的一個頂點.
恰好是該橢圓的一個頂點.
(1)求橢圓![]() 的方程;
的方程;
(2)已知直線![]() :
:![]() 與圓
與圓![]() :
:![]() 相切,且直線
相切,且直線![]() 與橢圓相交于
與橢圓相交于![]() 、
、![]() 兩點,求
兩點,求![]() 的值.
的值.
科目:高中數學 來源: 題型:
【題目】某市房產中心數據研究顯示,2018年該市新建住宅銷售均價如下表.3月至7月房價上漲過快,為抑制房價過快上漲,政府從8月份開始出臺了相關限購政策,10月份開始房價得到了很好的抑制.
均價(萬元/ | 0.95 | 0.98 | 1.11 | 1.12 | 1.20 | 1.22 | 1.32 | 1.34 | 1.16 | 1.06 |
月份 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
(Ⅰ)請建立3月至7月線性回歸模型(保留小數點后3位),并預測若政府不宏觀調控,12月份該市新建住宅銷售均價;
(Ⅱ)試用相關系數說明3月至7月各月均價![]() (萬元/
(萬元/![]() )與月份
)與月份![]() 之間可用線性回歸模型(保留小數點后2位)
之間可用線性回歸模型(保留小數點后2位)
參考數據:![]() ,
,![]() ,
,![]()
![]() ,
,![]() ,
,![]()
回歸方程斜率和截距最小二乘法估計公式 ;
;
相關系數 .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在直角坐標系![]() 中,以坐標原點為極點,
中,以坐標原點為極點,![]() 軸正半軸為極軸建立極坐標系,曲線
軸正半軸為極軸建立極坐標系,曲線![]() 的參數方程為
的參數方程為![]() (
(![]() 為參數),直線
為參數),直線![]() 經過點
經過點![]() 且傾斜角為
且傾斜角為![]() .
.
(1)求曲線![]() 的極坐標方程和直線
的極坐標方程和直線![]() 的參數方程;
的參數方程;
(2)已知直線![]() 與曲線
與曲線![]() 交于
交于![]() ,滿足
,滿足![]() 為
為![]() 的中點,求
的中點,求![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知點![]() ,點
,點![]() ,點
,點![]() ,動圓
,動圓![]() 與
與![]() 軸相切于點
軸相切于點![]() ,過點
,過點![]() 的直線
的直線![]() 與圓
與圓![]() 相切于點
相切于點![]() ,過點
,過點![]() 的直線
的直線![]() 與圓
與圓![]() 相切于點
相切于點![]() (
(![]() 均不同于點
均不同于點![]() ),且
),且![]() 與
與![]() 交于點
交于點![]() ,設點
,設點![]() 的軌跡為曲線
的軌跡為曲線![]() .
.
(1)證明:![]() 為定值,并求
為定值,并求![]() 的方程;
的方程;
(2)設直線![]() 與
與![]() 的另一個交點為
的另一個交點為![]() ,直線
,直線![]() 與
與![]() 交于
交于![]() 兩點,當
兩點,當![]() 三點共線時,求四邊形
三點共線時,求四邊形![]() 的面積.
的面積.
查看答案和解析>>
科目:高中數學 來源: 題型:
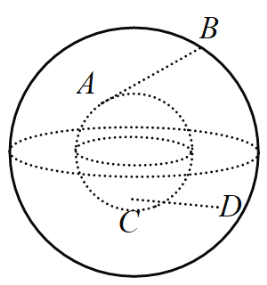
【題目】如圖兩個同心球,球心均為點![]() ,其中大球與小球的表面積之比為3:1,線段
,其中大球與小球的表面積之比為3:1,線段![]() 與
與![]() 是夾在兩個球體之間的內弦,其中
是夾在兩個球體之間的內弦,其中![]() 兩點在小球上,
兩點在小球上,![]() 兩點在大球上,兩內弦均不穿過小球內部.當四面體
兩點在大球上,兩內弦均不穿過小球內部.當四面體![]() 的體積達到最大值時,此時異面直線
的體積達到最大值時,此時異面直線![]() 與
與![]() 的夾角為
的夾角為![]() ,則
,則![]() ( )
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com