已知函數
·
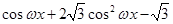（其中
>o），且函數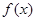
的最小正周期為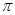
（I）求f（x）的最大值及相應x的取值
（Ⅱ）將函數y= f（x）的圖象向左平移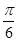
單位長度，再將所得圖象各點的橫坐標縮小為原來的
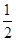倍（縱坐標不變）得到函數y=g（x）的圖象．求函數g（x）的單調區間．
科目：高中數學 來源： 題型：
(2)已知af(x)+bf(
)=cx(a、b、c∈R,ab≠0,a2≠b2),求f(x);
(3)f(x)是R上的奇函數，且x∈(-∞,0)時，f(x)=x2+2x,求f(x);
(4)某工廠生產一種機器的固定成本為5 000元，且每生產100部，需要增加投入2 500元，對銷售市場進行調查后得知，市場對此產品的需求量為每年500部，已知銷售收入的函數為H(x)=500x-
x2,其中x是產品售出的數量，且0≤x≤500.若x為年產量，y表示利潤，求y=f(x)的解析式.
查看答案和解析>>
科目：高中數學 來源： 題型：
(其中m、n、α、β∈R且α≠0)的圖象過點（0，-1），對稱中心是（1，1）.（1）試確定f(x)的解析式.
（2）如果數列{an}滿足：a1=3,an+1=f(an)(n∈N*),求{an}的通項公式.
（3）試探求形如f(x)的有理函數g(x)（異于f(x)），使得當數列{bn}滿足：b1=3,bn+1=g(bn)時，總有b2n-1=a2n-1(n∈N*)，并寫出兩個符合條件的函數.
查看答案和解析>>
科目：高中數學 來源： 題型：
已知函數
，
，其中m∈R．
（1）若0<m≤2，試判斷函數f (x)=f1 (x)+f2 (x)
的單調性，并證明你的結論；
（2）設函數
若對任意大于等于2的實數x1，總存在唯一的小于2的實數x2，使得g (x1) = g (x2) 成立，試確定實數m的取值范圍．
查看答案和解析>>
科目：高中數學 來源：2011-2012學年浙江省溫州市高三八校聯考理科數學 題型：填空題
已知函數
，
，其中a為常數，且函數y＝f(x)和y＝g(x)的圖像在其與兩坐標軸的交點處的切線相互平行．若關于x的不等式
對任意不等于1的正實數都成立，則實數m的取值集合是____________。
查看答案和解析>>
科目：高中數學 來源：2012-2013學年四川省成都市高新區高三（上）12月統考數學試卷（理科）（解析版） 題型：解答題
，
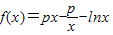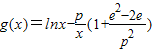，其中e=2.71828…．查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
的增區間為[
] 
;減區間為[
]，
， 2分
，函數
周期為
，所以
，
4分
， f（x）的最大值為2，對應x的取值是x=
. 將函數
的圖象向左平移
個單位后得到函數
的圖象，再將所得圖象各點的橫坐標縮小為原來的
倍，縱坐標不變，得到函數
.
9分
，
