【題目】已知函數
（1）證明：當
時， 
；
（2）若當
時， 
，求實數
的取值范圍.
【答案】（1）見解析；（2）見解析.
【解析】試題分析：（1）先求導數，再求導函數零點，列表分析函數單調性變化規律，確定函數最小值為
，即證得結論（2）先討論分母正負，化分式為整式，再求
導數，由于
，所以
必須為增函數，根據單調性討論可得實數
的取值范圍.
試題解析：（1）當
時， 
，
則
，令
，解得
當
時， 
，∴
在
上是減函數；
當
時， 
，∴
在
上是增函數；
故
在
處取得最小值
，即
.
（2）由已知
，∴
.
（i）當
時，若
，則
，此時
，不符合題設條件；
（ii）當
時，若
， 
令
，則
而
.
①當
時，由（1）知， 
，即
，
它等價于
， 
∴
此時
在
上是增函數，
∴
，即
.
②當
時，由（1）知， 
，∴ 
∴
當
時， 
，此時
在
上是減函數，
∴
，即
，不符合題設條件.
綜上: 
.
各地期末復習特訓卷系列答案
小博士期末闖關100分系列答案科目：高中數學 來源： 題型：
【題目】設函數f(x)＝|x＋2|＋|x－2|，x∈R，不等式f(x)≤6的解集為M.
（1）求M；
（2）當a2，b2∈M時，證明： 
|a＋b|≤|ab＋3|.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某學校為進行“陽光運動一小時”活動，計劃在一塊直角三角形
的空地上修建一個占地面積為
（平方米）的矩形
健身場地。如圖，點
在
上，點
在
上，且
點在斜邊
上，已知
米，
米，
，設矩形健身場地每平方米的造價為
元，再把矩形以外（陰影部分）鋪上草坪，每平方米的造價為
元（
為正的常數）.
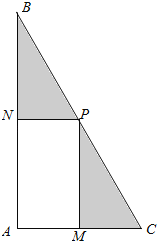
（1）試用
表示，并指出如何設計矩形的長和寬，才能使得矩形的面積最大，且求出的最大值；
（2）求總造價
關于面積的函數
，說明如何選取
，使總造價最低（不要求求出最低造價）.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知拋物線的頂點在原點,過點A(-4,4)且焦點在x軸.
（1）求拋物線方程;
（2）直線l過定點B(-1,0)與該拋物線相交所得弦長為8,求直線l的方程.
查看答案和解析>>
科目：高中數學 來源： 題型：
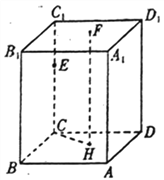
【題目】如圖所示，直平行六面體
中，
為棱
上任意一點，
為底面
（除
外）上一點，已知在底面
上的射影為
，若再增加一個條件，就能得到
，現給出以下條件：
①
；②在
上；③
平面
；④直線
和
在平面的射影為同一條直線．其中一定能成為增加條件的是__________．（把你認為正確的都填上）
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】一盒中裝有9張各寫有一個數字的卡片，其中4張卡片上的數字是1，3張卡片上的數字是2，2張卡片上的數字是3，從盒中任取3張卡片．
（Ⅰ）求所取3張卡片上的數字完全相同的概率；
（Ⅱ）
表示所取3張卡片上的數字的中位數，求
的分布列與數學期望．
（注：若三個數
滿足
，則稱
為這三個數的中位數）．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】（本小題共14分）如圖，在三棱錐
中， 
底面
，點
， 
分別在棱
上，且
（Ⅰ）求證： 
平面
；（Ⅱ）當
為
的中點時，求
與平面
所成的角的大小；（Ⅲ）是否存在點
使得二面角
為直二面角？并說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
