
【題目】極坐標系的極點在平面直角坐標系的原點O處,極軸與x軸的正半軸重合,兩坐標系單位長度相同.已知曲線的極坐標方程為ρ=2cosθ+2sinθ,直線l的參數方程為 ![]() (t為參數).
(t為參數).
(Ⅰ)將直線l的參數方程化為普通方程,將曲線C的極坐標方程化為直角坐標方程;
(Ⅱ)設曲線C上到直線l的距離為d的點的個數為f(d),求f(d)的解析式.
【答案】解:(Ⅰ)直線l的參數方程為 ![]() (t為參數),消去參數,可得普通方程x+y﹣1=0;
(t為參數),消去參數,可得普通方程x+y﹣1=0;
曲線的極坐標方程為ρ=2cosθ+2sinθ,即ρ2=2ρcosθ+2ρsinθ,∴x2+y2﹣2x﹣2y=0;
(Ⅱ)x2+y2﹣2x﹣2y=0,可化為(x﹣1)2+(y﹣1)2=2,
圓心C(1,1)到直線l的距離為 ![]() =
= ![]() ,圓的半徑為
,圓的半徑為 ![]() ,
,
圓上的點到直線l距離d的取值范圍是0≤d≤ ![]()
∴f(d)= 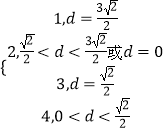
【解析】(Ⅰ)將直線l的參數方程消去參數,可得普通方程,將曲線C的極坐標方程,即ρ2=2ρcosθ+2ρsinθ,即可化為直角坐標方程;(Ⅱ)圓心C(1,1)到直線l的距離為 ![]() =
= ![]() ,圓的半徑為
,圓的半徑為 ![]() ,圓上的點到直線l距離d的取值范圍是0≤d≤
,圓上的點到直線l距離d的取值范圍是0≤d≤ ![]() ,即可求f(d)的解析式.
,即可求f(d)的解析式.


科目:高中數學 來源: 題型:
【題目】甲、乙兩人玩猜數字游戲,先由甲心中想一個數字,記為![]() ,再由乙猜甲剛才所想的數字,把乙猜的數字記為
,再由乙猜甲剛才所想的數字,把乙猜的數字記為![]() ,其中
,其中![]() ,若
,若![]() ,就稱甲乙“心有靈犀”.現任意找兩人玩這個游戲,則他們“心有靈犀”的概率為 ( )
,就稱甲乙“心有靈犀”.現任意找兩人玩這個游戲,則他們“心有靈犀”的概率為 ( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,設橢圓的中心為原點![]() ,長軸在
,長軸在![]() 軸上,上頂點為
軸上,上頂點為![]() ,左、右焦點分別為
,左、右焦點分別為![]() ,線段
,線段![]() 的中點分別為
的中點分別為![]() ,且
,且![]() 是面積為
是面積為![]() 的直角三角形.
的直角三角形.

(1)求該橢圓的離心率和標準方程;
(2)過![]() 作直線交橢圓于
作直線交橢圓于![]() 兩點,使
兩點,使![]() ,求
,求![]() 的面積.
的面積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() 是定義在
是定義在![]() 上的偶函數,且當
上的偶函數,且當![]() 時,
時,![]() .
.

(1)已畫出函數![]() 在
在![]() 軸左側的圖像,如圖所示,請補出完整函數
軸左側的圖像,如圖所示,請補出完整函數![]() 的圖像,并根據圖像寫出函數
的圖像,并根據圖像寫出函數![]() 的增區間;
的增區間;
⑵寫出函數![]() 的解析式和值域.
的解析式和值域.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】橢圓E: ![]() (a>b>0)的左右焦點分別為F1、F2 , D為橢圓短軸上的一個頂點,DF1的延長線與橢圓相交于G.△DGF2的周長為8,|DF1|=3|GF1|.
(a>b>0)的左右焦點分別為F1、F2 , D為橢圓短軸上的一個頂點,DF1的延長線與橢圓相交于G.△DGF2的周長為8,|DF1|=3|GF1|.
(Ⅰ)求橢圓E的方程;
(Ⅱ)過橢圓E的左頂點A作橢圓E的兩條互相垂直的弦AB、AC,試問直線BC是否恒過定點?若是,求出此定點的坐標;若不是,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】將函數 ![]() 的圖象向左平移
的圖象向左平移 ![]() 個單位,再向下平移4個單位,得到函數g(x)的圖象,則函數f(x)的圖象與函數g(x)的圖象( )
個單位,再向下平移4個單位,得到函數g(x)的圖象,則函數f(x)的圖象與函數g(x)的圖象( )
A.關于點(﹣2,0)對稱
B.關于點(0,﹣2)對稱
C.關于直線x=﹣2對稱
D.關于直線x=0對稱
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在三棱錐A﹣BCD中,側棱AB,AC,AD兩兩垂直,△ABC、△ACD、△ABD的面積分別為 ![]() 、
、 ![]() 、2
、2 ![]() ,則三棱錐A﹣BCD的外接球的體積為 .
,則三棱錐A﹣BCD的外接球的體積為 .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某地區10名健康兒童頭發和血液中的硒含量(單位:μg/ml)如下表所示:
血硒x | 74 | 66 | 88 | 69 | 91 | 73 | 66 | 96 | 58 | 73 |
發硒y | 13 | 10 | 13 | 11 | 16 | 9 | 7 | 14 | 5 | 10 |
(1)畫出散點圖;
(2)求回歸方程;
(3)若某名健康兒童的血液中的硒含量為94 μg/ml,預測他的發硒含量.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com