
如圖所示,AC為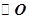 的直徑,D為
的直徑,D為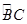 的中點,E為BC的中點.
的中點,E為BC的中點.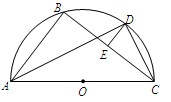
(Ⅰ)求證:AB∥DE;
(Ⅱ)求證:2AD·CD=AC·BC.
(Ⅰ)詳見解析;(Ⅱ)詳見解析.
解析試題分析:(Ⅰ)通過連接BD,通過證明與同一條直線垂直的兩條直線垂直的思路進行證明線線平行;(Ⅱ)通過證明△DAC∽△ECD,
試題解析:(Ⅰ)連接BD,因為D為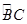 的中點,所以BD=DC.因為E為BC的中點,所以DE⊥BC.
的中點,所以BD=DC.因為E為BC的中點,所以DE⊥BC.
因為AC為圓的直徑,所以∠ABC=90°,所以AB∥DE. 5分
(Ⅱ)因為D為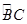 的中點,所以∠BAD=∠DAC,
的中點,所以∠BAD=∠DAC,
又∠BAD=∠DCB,則∠DAC=∠DCB.
又因為AD⊥DC,DE⊥CE,所以△DAC∽△ECD.
所以 =
= ,AD·CD=AC·CE,2AD·CD=AC·2CE,
,AD·CD=AC·CE,2AD·CD=AC·2CE,
因此2AD·CD=AC·BC. 10分
考點:1.線線平行的證明;2.三角形相似的證明.


科目:高中數學 來源: 題型:解答題
已知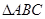 中,
中, ,
, ,
, 為
為 的中點,
的中點,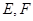 分別在線段
分別在線段 上,且
上,且
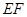 交
交 于
于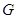 ,把
,把 沿
沿 折起,如下圖所示,
折起,如下圖所示,

(1)求證: 平面
平面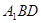 ;
;
(2)當二面角 為直二面角時,是否存在點
為直二面角時,是否存在點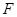 ,使得直線
,使得直線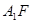 與平面
與平面 所成的角為
所成的角為 ,若存在求
,若存在求 的長,若不存在說明理由.
的長,若不存在說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
如圖已知:菱形 所在平面與直角梯形
所在平面與直角梯形 所在平面互相垂直,
所在平面互相垂直, ,
, 點
點 分別是線段
分別是線段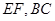 的中點.
的中點. 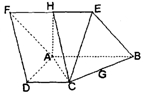
(1)求證:平面
 平面
平面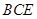 ;
;
(2)點 在直線
在直線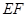 上,且
上,且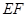 //平面
//平面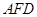 ,求平面
,求平面 與平面
與平面 所成角的余弦值。
所成角的余弦值。
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com