
【題目】已知函數![]() ,
,![]() .
.
(1)討論![]() 的單調性;
的單調性;
(2)若![]() ,證明:當
,證明:當![]() 時,
時,![]() .
.
【答案】(1)見解析(2)見解析
【解析】
(1)求函數導數,討論a,根據導數的正負分析函數單調性即可;
(2)要證![]() 在
在![]() 上恒成立,即證明
上恒成立,即證明![]() ,
,![]() 在
在![]() 上恒成立,設
上恒成立,設![]() ,求函數導數,利用單調性求最值證明即可.
,求函數導數,利用單調性求最值證明即可.
(1)![]()
當![]() 時,
時,![]()
當![]() 時,
時,![]() ,
,![]() 單調遞減,
單調遞減,
當![]() 時,
時,![]() ,
,![]() 單調遞增,
單調遞增,
所以![]() 在
在![]() 上單調遞減,在
上單調遞減,在![]() 上單調遞增.
上單調遞增.
當![]() 時,令
時,令![]() 得
得 ![]() (*)
(*)
因為![]() 所以方程(*)有兩根,由求根公式得
所以方程(*)有兩根,由求根公式得![]() ,
,![]() .
.
當![]() 時,
時,![]() , 當
, 當![]() 或
或![]() 時,
時,![]() ,
,![]() 單調遞減,
單調遞減,
當![]() 時,
時,![]() ,
,![]() 單調遞增,
單調遞增,
所以![]() 在
在![]() 和
和![]() 上單調遞減,在
上單調遞減,在![]() 上單調遞增.
上單調遞增.
當![]() 時,
時,![]() , 當
, 當![]() 或
或![]() 時,
時,![]() ,
,![]() 單調遞增,當
單調遞增,當![]() 時,
時,![]() ,
,![]() 單調遞減,
單調遞減,
所以![]() 在
在![]() 和
和![]() 上單調遞增,在
上單調遞增,在![]() 上單調遞減.
上單調遞減.
綜上所述,當![]() 時,
時,![]() 在
在![]() 上單調遞減,在
上單調遞減,在![]() 上單調遞增;
上單調遞增;
當![]() 時,
時,![]() 在
在![]() 和
和![]() 上單調遞減,在
上單調遞減,在![]() 上單調遞增;
上單調遞增;
當![]() 時,
時,![]() 在
在![]() 和
和![]() 上單調遞增,在
上單調遞增,在![]() 上單調遞減.
上單調遞減.
(2)當![]() 時,
時,![]() ,由題意知,要證
,由題意知,要證![]() 在
在![]() 上恒成立,
上恒成立,
即證明![]() ,
,![]() 在
在![]() 上恒成立.
上恒成立.
設![]() ,則
,則![]() ,
,
因為![]() ,所以
,所以![]() ,
,![]() (當且僅當
(當且僅當![]() 時等號成立),
時等號成立),
即![]() ,
,
所以![]() 在
在![]() 上單調遞增,
上單調遞增,![]() ,
,
所以![]() 在
在![]() 上恒成立.
上恒成立.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】某市為制定合理的節電方案,對居民用電情況進行了調查,通過抽樣,獲得了某年200戶居民每戶的月均用電量(單位:百度),將數據按照![]() ,
,![]() ,
,![]() 分成
分成![]() 組,制成了如圖所示的頻率分布直方圖:
組,制成了如圖所示的頻率分布直方圖:

(I)求直方圖中![]() 的值;
的值;
56789月均用電量百廈
(Ⅱ)設該市有100萬戶居民,估計全市每戶居民中月均用電量不低于6百度的人數,估計每戶居民月均用電量的中位數,說明理由;
(Ⅲ)政府計劃對月均用電量在4(百度)以下的用戶進行獎勵,月均用電量在![]() 內的用戶獎勵20元/月,月均用電量在
內的用戶獎勵20元/月,月均用電量在![]() 內的用戶獎勵10元/月,月均用電量在
內的用戶獎勵10元/月,月均用電量在![]() 內的用戶獎勵2元/月.若該市共有400萬戶居民,試估計政府執行此計劃的年度預算.
內的用戶獎勵2元/月.若該市共有400萬戶居民,試估計政府執行此計劃的年度預算.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() ,點
,點![]() 為橢圓上一點,且
為橢圓上一點,且![]() .
.
(1)求橢圓C的方程;
(2)已知兩條互相垂直的直線![]() ,
,![]() 經過橢圓
經過橢圓![]() 的右焦點
的右焦點![]() ,與橢圓
,與橢圓![]() 交于
交于![]() 四點,求四邊形
四點,求四邊形![]() 面積的的取值范圍.
面積的的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖是某公司2001年至2017年新產品研發費用![]() (單位:萬元)的折線圖.為了預測該公司2019年的新產品研發費用,建立了
(單位:萬元)的折線圖.為了預測該公司2019年的新產品研發費用,建立了![]() 與時間變量
與時間變量![]() 的兩個線性回歸模型.根據2001年至2017年的數據(時間變量
的兩個線性回歸模型.根據2001年至2017年的數據(時間變量![]() 的值依次為1,2,…,17)建立模型①:
的值依次為1,2,…,17)建立模型①:![]() ;根據2011年至2017年的數據(時間變量
;根據2011年至2017年的數據(時間變量![]() 的值依次為1,2,…,7)建立模型②:
的值依次為1,2,…,7)建立模型②:![]() .
.

(1)分別利用這兩個模型,求該公司2019年的新產品研發費用的預測值;
(2)你認為用哪個模型得到的預測值更可靠?并說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,ABCD﹣A1B1C1D1為正方體,則以下結論:①BD∥平面CB1D1;②AC1⊥BD;③AC1⊥平面CB1D1其中正確結論的個數是( )
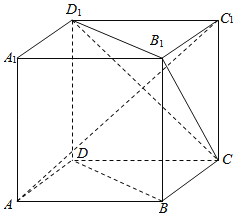
A.0B.1C.2D.3
查看答案和解析>>
科目:高中數學 來源: 題型:
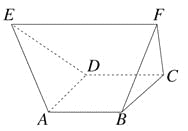
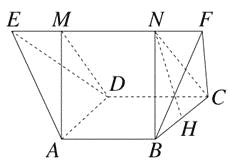
【題目】如圖,在多面體ABCDEF中,已知四邊形ABCD是邊長為1的正方形,且△ADE,△BCF均為正三角形,EF∥AB,EF=2,則該多面體的體積為( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】對于定義在![]() 上的函數
上的函數![]() ,若函數
,若函數![]() 滿足:①在區間
滿足:①在區間![]() 上單調遞減,②存在常數
上單調遞減,②存在常數![]() ,使其值域為
,使其值域為![]() ,則稱函數
,則稱函數![]() 是函數
是函數![]() 的“漸近函數”.
的“漸近函數”.
(1)判斷函數![]() 是不是函數
是不是函數![]() 的“漸近函數”,說明理由;
的“漸近函數”,說明理由;
(2)求證:函數![]() 不是函數
不是函數![]() 的“漸近函數”;
的“漸近函數”;
(3)若函數![]() ,
,![]() ,求證:當且僅當
,求證:當且僅當![]() 時,
時,![]() 是
是![]() 的“漸近函數”.
的“漸近函數”.
查看答案和解析>>
科目:高中數學 來源: 題型:
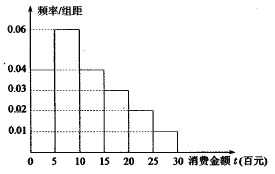
【題目】“雙十一”已經成為網民們的網購狂歡節,某電子商務平臺對某市的網民在今年“雙十一”的網購情況進行摸底調查,用隨機抽樣的方法抽取了100人,其消費金額![]() (百元)的頻率分布直方圖如圖所示:
(百元)的頻率分布直方圖如圖所示:
(1)求網民消費金額![]() 的平均值和中位數
的平均值和中位數![]() ;
;
(2)把下表中空格里的數填上,能否有![]() 的把握認為網購消費與性別有關;
的把握認為網購消費與性別有關;
男 | 女 | 合計 | |
| |||
| 30 | ||
合計 | 45 |
附表:
|
|
|
|
|
|
|
|
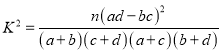 .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com