
【題目】某工廠對(duì)新研發(fā)的一種產(chǎn)品進(jìn)行試銷(xiāo),得到如下數(shù)據(jù)表:

(1)根據(jù)上表求出回歸直線(xiàn)方程![]() ,并預(yù)測(cè)當(dāng)單價(jià)定為8.3元時(shí)的銷(xiāo)量;
,并預(yù)測(cè)當(dāng)單價(jià)定為8.3元時(shí)的銷(xiāo)量;
(2)如果該工廠每件產(chǎn)品的成本為5.5元,利用所求的回歸方程,要使得利潤(rùn)最大,單價(jià)應(yīng)該定為多少?
附:線(xiàn)性回歸方程![]() 中斜率和截距最小二乘估計(jì)計(jì)算公式:
中斜率和截距最小二乘估計(jì)計(jì)算公式:
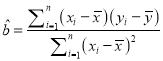 ,
, ![]()
【答案】(1)![]() ,84(2)9
,84(2)9
【解析】試題分析:(1)依次算出![]() ,
, ![]() ,代入
,代入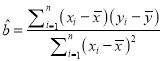 和
和![]() ,可求得線(xiàn)性回歸方程,代科
,可求得線(xiàn)性回歸方程,代科![]() 時(shí),解得
時(shí),解得![]() 預(yù)測(cè)單價(jià)。(2)由(1)得回歸直線(xiàn)方程為
預(yù)測(cè)單價(jià)。(2)由(1)得回歸直線(xiàn)方程為![]()
利潤(rùn)![]()
![]() ,為二次函數(shù),可知對(duì)稱(chēng)軸時(shí)利潤(rùn)最大。
,為二次函數(shù),可知對(duì)稱(chēng)軸時(shí)利潤(rùn)最大。
試題解析:(1)由已知得![]()
![]()
代入斜率估計(jì)公式可得![]() ,
,
將![]() 代入得
代入得![]()
所以回歸直線(xiàn)方程為![]() ,
,
當(dāng)![]() 時(shí),解得
時(shí),解得![]() 。即預(yù)測(cè)單價(jià)定為8.3元時(shí)的銷(xiāo)量為84(百件)
。即預(yù)測(cè)單價(jià)定為8.3元時(shí)的銷(xiāo)量為84(百件)
(2)利潤(rùn)![]()
![]()
對(duì)稱(chēng)軸為![]() ,所以要使得利潤(rùn)最大,單價(jià)應(yīng)該定為9元。
,所以要使得利潤(rùn)最大,單價(jià)應(yīng)該定為9元。


 智趣暑假溫故知新系列答案
智趣暑假溫故知新系列答案 英語(yǔ)小英雄天天默寫(xiě)系列答案
英語(yǔ)小英雄天天默寫(xiě)系列答案 暑假作業(yè)安徽少年兒童出版社系列答案
暑假作業(yè)安徽少年兒童出版社系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】函數(shù)f(x)的定義域?yàn)?0,+∞),且對(duì)一切x>0,y>0都有![]() ,當(dāng)
,當(dāng)![]() 時(shí),有
時(shí),有![]()
(1)求f(1)的值;
(2)判斷f(x)的單調(diào)性并加以證明;
(3)若f(4)=2,求f(x)在[1,16]上的值域.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】設(shè)直線(xiàn)![]() 經(jīng)過(guò)點(diǎn)
經(jīng)過(guò)點(diǎn)![]() 傾斜角為
傾斜角為![]() .(10分).
.(10分).
(1)寫(xiě)出直線(xiàn)![]() 的參數(shù)方程
的參數(shù)方程
(2)求直線(xiàn)![]() 與直線(xiàn)
與直線(xiàn)![]() 的交點(diǎn)到點(diǎn)
的交點(diǎn)到點(diǎn)![]() 的距離
的距離
(3)設(shè)![]() 與圓
與圓![]()
![]() 相交于兩點(diǎn)
相交于兩點(diǎn)![]() ,求點(diǎn)
,求點(diǎn)![]() 到
到![]() 兩點(diǎn)的距離的和與積。
兩點(diǎn)的距離的和與積。
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】《中國(guó)詩(shī)詞大會(huì)》是中央電視臺(tái)最近推出的一檔有重大影響力的大型電視文化節(jié)目,今年兩會(huì)期間,教育部部長(zhǎng)陳寶生答記者問(wèn)時(shí)就給予其高度評(píng)價(jià).基于這樣的背景,山東某中學(xué)積極響應(yīng),也舉行了一次詩(shī)詞競(jìng)賽.組委會(huì)在競(jìng)賽后,從中抽取了部分選手的成績(jī)(百分制),作為樣本進(jìn)行統(tǒng)計(jì),作出了圖1的頻率分布直方圖和圖2的莖葉圖(但中間三行污損,看不清數(shù)據(jù)).
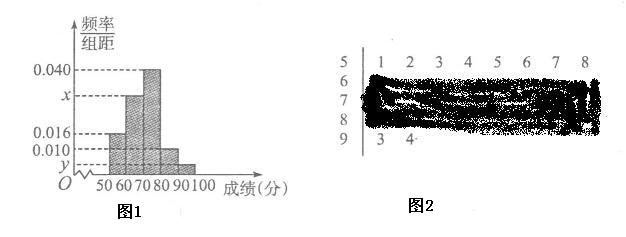
(I)求樣本容量![]() 和頻率分布直方圖中的
和頻率分布直方圖中的![]() ,
,![]() 的值;
的值;
(II)分?jǐn)?shù)在[80,90)的學(xué)生中,男生有2人,現(xiàn)從該組抽取三人“座談”,寫(xiě)出基本事件空間并求至少有兩名女生的概率.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知{an}是公差為1的等差數(shù)列,a1 , a5 , a25成等比數(shù)列.
(1)求數(shù)列{an}的通項(xiàng)公式;
(2)設(shè)bn= ![]() 3+an , 求數(shù)列{bn}的前n項(xiàng)和Tn .
3+an , 求數(shù)列{bn}的前n項(xiàng)和Tn .
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,已知拋物線(xiàn)![]() :
:![]() ,過(guò)焦點(diǎn)
,過(guò)焦點(diǎn)![]() 斜率大于零的直線(xiàn)
斜率大于零的直線(xiàn)![]() 交拋物線(xiàn)于
交拋物線(xiàn)于![]() 、
、![]() 兩點(diǎn),且與其準(zhǔn)線(xiàn)交于點(diǎn)
兩點(diǎn),且與其準(zhǔn)線(xiàn)交于點(diǎn)![]() .
.

(Ⅰ)若線(xiàn)段![]() 的長(zhǎng)為
的長(zhǎng)為![]() ,求直線(xiàn)
,求直線(xiàn)![]() 的方程;
的方程;
(Ⅱ)在![]() 上是否存在點(diǎn)
上是否存在點(diǎn)![]() ,使得對(duì)任意直線(xiàn)
,使得對(duì)任意直線(xiàn)![]() ,直線(xiàn)
,直線(xiàn)![]() ,
,![]() ,
,![]() 的斜率始終成等差數(shù)列,若存在求點(diǎn)
的斜率始終成等差數(shù)列,若存在求點(diǎn)![]() 的坐標(biāo);若不存在,請(qǐng)說(shuō)明理由.
的坐標(biāo);若不存在,請(qǐng)說(shuō)明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知函數(shù)![]() ,(
,( ![]() )
)
(1)當(dāng)![]() 時(shí),求函數(shù)
時(shí),求函數(shù)![]() 在
在![]() 處的切線(xiàn)方程;
處的切線(xiàn)方程;
(2)若函數(shù)![]() 在區(qū)間
在區(qū)間![]() 上單調(diào)遞增,求
上單調(diào)遞增,求![]() 的取值范圍;
的取值范圍;
(3)求函數(shù)![]() 在區(qū)間
在區(qū)間![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知等差數(shù)列{an}中,a1=1,a3=﹣3.
(1)求數(shù)列{an}的通項(xiàng)公式;
(2)若數(shù)列{an}的前k項(xiàng)和Sk=﹣35,求k的值.
查看答案和解析>>
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專(zhuān)區(qū) | 電信詐騙舉報(bào)專(zhuān)區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專(zhuān)區(qū) | 涉企侵權(quán)舉報(bào)專(zhuān)區(qū)
違法和不良信息舉報(bào)電話(huà):027-86699610 舉報(bào)郵箱:58377363@163.com