
【題目】已知橢圓![]() :
:![]() 的右頂點為
的右頂點為![]() ,離心率為
,離心率為![]() ,點
,點![]() 在橢圓上,點
在橢圓上,點![]() 與點
與點![]() 關于原點對稱.
關于原點對稱.
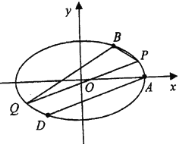
(1)求橢圓![]() 的標準方程;
的標準方程;
(2)求經過點![]() ,
,![]() 且和
且和![]() 軸相切的圓的方程;
軸相切的圓的方程;
(3)若![]() ,
,![]() 是橢圓上異于
是橢圓上異于![]() ,
,![]() 的兩個點,且
的兩個點,且![]() ,點
,點![]() 在直線
在直線![]() 的上方,試判斷
的上方,試判斷![]() 的平分線是否經過
的平分線是否經過![]() 軸上的一個定點?若是,求出該定點坐標;若不是,請說明理由.
軸上的一個定點?若是,求出該定點坐標;若不是,請說明理由.
【答案】(1)![]() ;(2)
;(2)![]() 或
或![]() ;(3)是,
;(3)是,![]() .
.
【解析】
(1)根據點![]() 的坐標滿足橢圓方程,結合離心率即可求得橢圓方程;
的坐標滿足橢圓方程,結合離心率即可求得橢圓方程;
(2)由(1)中所求即可知![]() 點坐標,設出直線方程,根據題意,列方程求解即可;
點坐標,設出直線方程,根據題意,列方程求解即可;
(3)設出直線![]() 、
、![]() 的斜率分別為
的斜率分別為![]() 、
、![]() ,以及兩條直線的方程,聯立橢圓方程,根據韋達定理,求得
,以及兩條直線的方程,聯立橢圓方程,根據韋達定理,求得![]() 兩點的坐標,結合
兩點的坐標,結合![]() //
//![]() ,找到
,找到![]() 之間的關系,即可容易求得.
之間的關系,即可容易求得.
(1)由 ,解得
,解得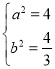 ,
,
所以橢圓的標準方程為![]() :
:![]() .
.
(2)設經過點![]() ,
,![]() 且和
且和![]() 軸相切的圓的圓心為
軸相切的圓的圓心為![]() ,半徑為
,半徑為![]() ,
,
圓的方程為![]() ,由題意可知
,由題意可知![]() ,因為
,因為![]() ,
,![]() 在圓上,
在圓上,
所以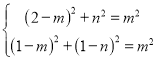 ,解得
,解得![]() 或
或![]() ,
,
故所求的圓的方程為![]() 或
或![]() .
.
(3)設點![]() 、
、![]() 分別為
分別為![]() 、
、![]() ,直線
,直線![]() 、
、![]() 的斜率分別為
的斜率分別為![]() 、
、![]() ,
,
聯立直線![]() 與橢圓方程
與橢圓方程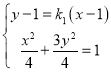 ,
,
化簡得![]() ,
,
∵![]() 是方程的一個解,∴
是方程的一個解,∴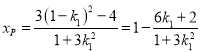 ,則
,則![]() ,
,
同理可得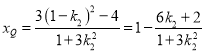 ,則
,則![]() ,
,
∴直線![]() 的斜率
的斜率![]() ,
,
又∵![]() 且
且![]() ,∴
,∴![]() ,化簡得
,化簡得![]() ,
,
∴直線![]() 、
、![]() 關于直線
關于直線![]() 對稱,即
對稱,即![]() 為
為![]() 的角平分線所在的直線,
的角平分線所在的直線,
∴![]() 的角平分線經過
的角平分線經過![]() 軸上的定點
軸上的定點![]() .
.


科目:高中數學 來源: 題型:
【題目】在某地區某高傳染性病毒流行期間,為了建立指標顯示疫情已受控制,以便向該地區居民顯示可以過正常生活,有公共衛生專家建議的指標是“連續7天每天新增感染人數不超過5人”,根據連續7天的新增病例數計算,下列各個選項中,一定符合上述指標的是__________.
①平均數![]() ; ②標準差
; ②標準差![]() ; ③平均數
; ③平均數![]() 且標準差
且標準差![]() ;
;
④平均數![]() 且極差小于或等于2; ⑤眾數等于1且極差小于或等于4.
且極差小于或等于2; ⑤眾數等于1且極差小于或等于4.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() ,右頂點為
,右頂點為![]() ,右焦點為
,右焦點為![]() ,
,![]() 為坐標原點,
為坐標原點,![]() ,橢圓
,橢圓![]() 過點
過點![]() .
.
(1)求橢圓![]() 的方程;
的方程;
(2)若過點![]() 的直線
的直線![]() 與橢圓
與橢圓![]() 交于不同的兩點
交于不同的兩點![]() (
(![]() 在
在![]() 之間),求
之間),求![]() 與
與![]() 面積之比的取值范圍.
面積之比的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某小學舉辦“父母養育我,我報父母恩”的活動,對六個年級(一年級到六年級的年級代碼分別為1,2…,6)的學生給父母洗腳的百分比y%進行了調查統計,繪制得到下面的散點圖.
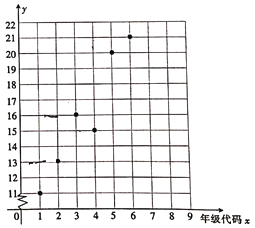
(1)由散點圖看出,可用線性回歸模型擬合y與x的關系,請用相關系數加以說明;
(2)建立y關于x的回歸方程,并據此預計該校學生升入中學的第一年(年級代碼為7)給父母洗腳的百分比.
附注:參考數據:![]()
參考公式:相關系數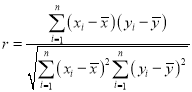 ,若r>0.95,則y與x的線性相關程度相當高,可用線性回歸模型擬合y與x的關系.回歸方程
,若r>0.95,則y與x的線性相關程度相當高,可用線性回歸模型擬合y與x的關系.回歸方程![]() 中斜率與截距的最小二乘估計公式分別為
中斜率與截距的最小二乘估計公式分別為![]() =
=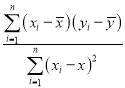 ,
,![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() (其中
(其中![]() 是常數,且
是常數,且![]() ),曲線
),曲線![]() 在
在![]() 處的切線方程為
處的切線方程為![]() .
.
(1)求![]() 的值;
的值;
(2)若存在![]() (其中
(其中![]() 是自然對數的底),使得
是自然對數的底),使得![]() 成立,求
成立,求![]() 的取值范圍;
的取值范圍;
(3)設![]() ,若對任意
,若對任意![]() ,均存在
,均存在![]() ,使得方程
,使得方程![]() 有三個不同的實數解,求實數
有三個不同的實數解,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的右焦點為
的右焦點為![]() .直線
.直線![]() 被稱作為橢圓
被稱作為橢圓![]() 的一條準線.點
的一條準線.點![]() 在橢圓
在橢圓![]() 上(異于橢圓左、右頂點),過點
上(異于橢圓左、右頂點),過點![]() 作直線
作直線![]() 與橢圓
與橢圓![]() 相切,且與直線
相切,且與直線![]() 相交于點
相交于點![]() .
.
(1)求證:![]() .
.
(2)若點![]() 在
在![]() 軸的上方,
軸的上方,![]() ,求
,求![]() 面積的最小值.
面積的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知點![]() 是拋物線
是拋物線![]() 上一點,點
上一點,點![]() 為拋物線
為拋物線![]() 的焦點,
的焦點,![]() .
.
(1)求直線![]() 的方程;
的方程;
(2)若直線![]() 與拋物線
與拋物線![]() 的另一個交點為
的另一個交點為![]() ,曲線
,曲線![]() 在點
在點![]() 與點
與點![]() 處的切線分別為
處的切線分別為![]() ,直線
,直線![]() 相交于點
相交于點![]() ,求點
,求點![]() 的坐標.
的坐標.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某大學開學期間,該大學附近一家快餐店招聘外賣騎手,該快餐店提供了兩種日工資結算方案:方案![]() 規定每日底薪100元,外賣業務每完成一單提成2元;方案
規定每日底薪100元,外賣業務每完成一單提成2元;方案![]() 規定每日底薪150元,外賣業務的前54單沒有提成,從第55單開始,每完成一單提成5元.該快餐店記錄了每天騎手的人均業務量,現隨機抽取100天的數據,將樣本數據分為
規定每日底薪150元,外賣業務的前54單沒有提成,從第55單開始,每完成一單提成5元.該快餐店記錄了每天騎手的人均業務量,現隨機抽取100天的數據,將樣本數據分為![]() 七組,整理得到如圖所示的頻率分布直方圖.
七組,整理得到如圖所示的頻率分布直方圖.
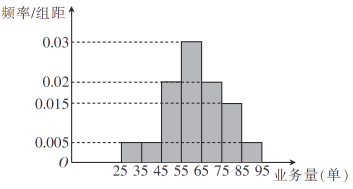
(1)隨機選取一天,估計這一天該快餐店的騎手的人均日外賣業務量不少于65單的概率;
(2)從以往統計數據看,新聘騎手選擇日工資方案![]() 的概率為
的概率為![]() ,選擇方案
,選擇方案![]() 的概率為
的概率為![]() .若甲、乙、丙、丁四名騎手分別到該快餐店應聘,四人選擇日工資方案相互獨立,求至少有兩名騎手選擇方案
.若甲、乙、丙、丁四名騎手分別到該快餐店應聘,四人選擇日工資方案相互獨立,求至少有兩名騎手選擇方案![]() 的概率,
的概率,
(3)若僅從人日均收入的角度考慮,請你為新聘騎手做出日工資方案的選擇,并說明理由.(同組中的每個數據用該組區間的中點值代替)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com