
【題目】某市計劃在一片空地上建一個集購物、餐飲、娛樂為一體的大型綜合園區,如圖,已知兩個購物廣場的占地都呈正方形,它們的面積分別為13公頃和8公頃;美食城和歡樂大世界的占地也都呈正方形,分別記它們的面積為![]() 公頃和
公頃和![]() 公頃;由購物廣場、美食城和歡樂大世界圍成的兩塊公共綠地都呈三角形,分別記它們的面積為
公頃;由購物廣場、美食城和歡樂大世界圍成的兩塊公共綠地都呈三角形,分別記它們的面積為![]() 公頃和
公頃和![]() 公頃.
公頃.
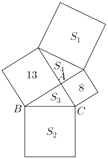
(1)設![]() ,用關于
,用關于![]() 的函數
的函數![]() 表示
表示![]() ,并求
,并求![]() 在區間
在區間![]() 上的最大值的近似值(精確到0.001公頃);
上的最大值的近似值(精確到0.001公頃);
(2)如果![]() ,并且
,并且![]() ,試分別求出
,試分別求出![]() 、
、![]() 、
、![]() 、
、![]() 的值.
的值.
 小學學習好幫手系列答案
小學學習好幫手系列答案 小學同步三練核心密卷系列答案
小學同步三練核心密卷系列答案科目:高中數學 來源: 題型:
【題目】隨著城市地鐵建設的持續推進,市民的出行也越來越便利.根據大數據統計,某條地鐵線路運行時,發車時間間隔t(單位:分鐘)滿足:4≤t≤15,![]() N,平均每趟地鐵的載客人數p(t)(單位:人)與發車時間間隔t近似地滿足下列函數關系:
N,平均每趟地鐵的載客人數p(t)(單位:人)與發車時間間隔t近似地滿足下列函數關系: ,其中
,其中![]() .
.
(1)若平均每趟地鐵的載客人數不超過1500人,試求發車時間間隔t的值.
(2)若平均每趟地鐵每分鐘的凈收益為![]() (單位:元),問當發車時間間隔t為多少時,平均每趟地鐵每分鐘的凈收益最大?井求出最大凈收益.
(單位:元),問當發車時間間隔t為多少時,平均每趟地鐵每分鐘的凈收益最大?井求出最大凈收益.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設數列![]() 的各項都是正數,若對于任意的正整數
的各項都是正數,若對于任意的正整數![]() ,存在
,存在![]() ,使得
,使得![]() 、
、![]() 、
、![]() 成等比數列,則稱函數
成等比數列,則稱函數![]() 為“
為“![]() 型”數列.
型”數列.
(1)若![]() 是“
是“![]() 型”數列,且
型”數列,且![]() ,
,![]() ,求
,求![]() 的值;
的值;
(2)若![]() 是“
是“![]() 型”數列,且
型”數列,且![]() ,
,![]() ,求
,求![]() 的前
的前![]() 項和
項和![]() ;
;
(3)若![]() 既是“
既是“![]() 型”數列,又是“
型”數列,又是“![]() 型”數列,求證:數列
型”數列,求證:數列![]() 是等比數列.
是等比數列.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=(2x-4)ex+a(x+2)2(x>0,a∈R,e是自然對數的底數).
(1)若f(x)是(0,+∞)上的單調遞增函數,求實數a的取值范圍;
(2)當a∈![]() 時,證明:函數f(x)有最小值,并求函數f(x)的最小值的取值范圍.
時,證明:函數f(x)有最小值,并求函數f(x)的最小值的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐P-ABCD中,AD∥BC,![]() ADC=
ADC=![]() PAB=90°,BC=CD=
PAB=90°,BC=CD=![]() AD.E為棱AD的中點,異面直線PA與CD所成的角為90°.
AD.E為棱AD的中點,異面直線PA與CD所成的角為90°.

(I)在平面PAB內找一點M,使得直線CM∥平面PBE,并說明理由;
(II)若二面角P-CD-A的大小為45°,求直線PA與平面PCE所成角的正弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知一列函數![]() ,設直線
,設直線![]() 與
與![]() 的交點為
的交點為![]() ,點
,點![]() 在
在![]() 軸和直線
軸和直線![]() 上的射影分別為
上的射影分別為![]() ,記
,記![]() 的面積為
的面積為![]() ,
,![]() 的面積為
的面積為![]() .
.
(1)求![]() 的最小值,并指出此時
的最小值,并指出此時![]() 的取值;
的取值;
(2)在![]() 中任取一個函數,求該函數在
中任取一個函數,求該函數在![]() 上是增函數或在
上是增函數或在![]() 上是減函數的概率;
上是減函數的概率;
(3)是否存在正整數![]() ,使得
,使得![]() 成立,若存在,求出
成立,若存在,求出![]() 的值,若不存在,請說明理由.
的值,若不存在,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com