
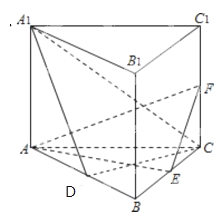
【題目】(2015·湖南)如圖,直三棱柱ABC-A1B1C1的底面是邊長為2的正三角形,E,F分別是BC,CC1的中點。
(1)證明:平面AEF⊥平面B1BCC1;
(2)若直線AC1與平面AA1BB1所成的角為45°,求三棱錐F-AEC的體積。
【答案】
(1)
略。
(2)
![]()
【解析】(I)如圖,因為三棱柱ABC-A1B1C1是直三棱柱,
所以AE⊥BB1 , 又E是正三角形的邊BC的中點,
ABC所以AE⊥BC,因此AE⊥平面B1BCC1 , 而AE![]() 平面AEF,
平面AEF,
所以平面AEF⊥平面B1BCC1。
(II)設AB的中點為D,連接A1DCD,因為△ABC是正三角形,所以CD⊥AB,又三棱柱ABC-A1B1C1是直三棱柱,所以,因此CD⊥平面A1AB1B,于是∠CA1D直線A1C與平面A1ABB1所成的角,由題設知∠CA1D=45°,
所以A1D=CD=![]() AB=
AB=![]() ,
,
在Rt△AA1D中,AA1=![]() =
=![]() =
=![]() ,所以FC=
,所以FC=![]() AA1=
AA1=![]()
故三棱錐F-AEC的體積V=![]() SAECxFC=
SAECxFC=![]() x
x![]() x
x![]() =
=![]() 。
。
【考點精析】解答此題的關鍵在于理解直線與平面垂直的判定的相關知識,掌握一條直線與一個平面內的兩條相交直線都垂直,則該直線與此平面垂直;注意點:a)定理中的“兩條相交直線”這一條件不可忽視;b)定理體現了“直線與平面垂直”與“直線與直線垂直”互相轉化的數學思想.


 優化作業上海科技文獻出版社系列答案
優化作業上海科技文獻出版社系列答案科目:高中數學 來源: 題型:
【題目】![]() 如圖,長方體ABCD-A1B1C1D1中,AB=16,BC=10,AA1=8,點E、F分別在A1B1、C1D1上,A1E=D1F=4,過點E,F的平面
如圖,長方體ABCD-A1B1C1D1中,AB=16,BC=10,AA1=8,點E、F分別在A1B1、C1D1上,A1E=D1F=4,過點E,F的平面![]() 與此長方體的面相交,交線圍成一個正方形。
與此長方體的面相交,交線圍成一個正方形。
(1)(Ⅰ)在圖中畫出這個正方形(不必說出畫法和理由);
(2)(Ⅱ)求直線AF與平面![]() 所成角的正弦值
所成角的正弦值
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(2015·四川)如圖,A , B , C , D為平面四邊形ABCD的四個內角.
(1)證明:tan![]() =
=![]()
(2)若A+C=180°, AB=6, BC=3, CD=4, AD=5, 求tan![]() +tan
+tan![]() +tan
+tan![]() +tan
+tan![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(2015·陜西)如圖1,在直角梯形ABCD中,AD∥BC,![]() BAD=
BAD=![]() ,AB=BC=1,
,AB=BC=1,
AD=2, E是AD的中點,0是AC與BE的交點.將△ABE沿BE折起到△A1BE的位置,如圖2.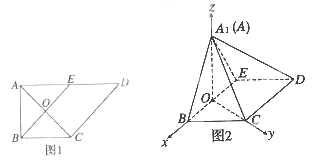
(1)證明:CD⊥平面A1OC
(2)若平面A1BE⊥平面BCDE, 四棱錐A1-BCDE的體積為36![]() ,求a的值.
,求a的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(2015·江蘇) 已知函數f(x)=x3+ax2+b(a,b![]() R).
R).
(1)試討論f(x)的單調性;
(2)若b=c-a(實數c是a與無關的常數),當函數f(x)有三個不同的零點時,a的取值范圍恰好是(-![]() ,-3)
,-3)![]() (1,
(1,![]() )
)![]() (
(![]() ,+
,+![]() ),求c的值.
),求c的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(2015·湖北)已知數列![]() 的各項均為正數,
的各項均為正數,![]() ,
, ![]() 為自然對數的底數.
為自然對數的底數.
(1)求函數![]() 的單調區間,并比較
的單調區間,并比較![]() 與
與![]() 的大小;
的大小;
(2)計算![]() ,
, ![]() ,
, ![]() , 由此推測計算
, 由此推測計算![]() 的公式,并給出證明;
的公式,并給出證明;
(3)令![]() , 數列
, 數列![]() ,
, ![]() 的前
的前![]() 項和分別記為
項和分別記為![]() ,
,![]() , 證明:
, 證明:![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】![]() 已知數列
已知數列![]() 是遞增的等比數列,a1+a4=9,a2a3=8,則數列
是遞增的等比數列,a1+a4=9,a2a3=8,則數列![]() 的前n項和等于
的前n項和等于![]() ,解得a1=1,a4=8,或者a1=8,a4=1,但由于是遞增數列,即a1=1,a4=8,即q3=
,解得a1=1,a4=8,或者a1=8,a4=1,但由于是遞增數列,即a1=1,a4=8,即q3=![]() =8,所以q=2.因而數列
=8,所以q=2.因而數列![]() 的前n項和為 。
的前n項和為 。
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com