【題目】選修4-4：坐標系與參數方程
以平面直角坐標系
的原點為極點，
軸的正半軸為極軸，建立極坐標系，且兩種坐標系中采取相同的單位長度.曲線
的極坐標方程是
，直線的參數方程是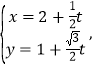
（
為參數）.
（1）求曲線的直角坐標方程與直線
的普通方程；
（2）設點
，若直線與曲線交于
兩點，求
的值.
閱讀快車系列答案科目：高中數學 來源： 題型：
【題目】隨著智能手機的普及，使用手機上網成為了人們日常生活的一部分，很多消費者對手機流量的需求越來越大.長沙某通信公司為了更好地滿足消費者對流量的需求，準備推出一款流量包.該通信公司選了5個城市（總人數、經濟發展情況、消費能力等方面比較接近）采用不同的定價方案作為試點，經過一個月的統計，發現該流量包的定價
:(單位：元/月）和購買人數
(單位：萬人）的關系如表:
（1）根據表中的數據，運用相關系數進行分析說明，是否可以用線性回歸模型擬合與的關系？并指出是正相關還是負相關；
（2）①求出關于的回歸方程；
②若該通信公司在一個類似于試點的城市中將這款流量包的價格定位25元/ 月，請用所求回歸方程預測長沙市一個月內購買該流量包的人數能否超過20 萬人.
參考數據：
，
，
.
參考公式：相關系數
，回歸直線方程
，
其中
，
.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】下列命題中，正確的選項是（ ）
A. 若
為真命題，則
為真命題 B. 
，使得
C. “平面向量
與
的夾角為鈍角”的充分不必要條件是“
” D. 在銳角
中，必有
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】過圓
：
上一動點
作
軸的垂線，交軸于點
，點
滿足
.
（Ⅰ）求點的軌跡方程；
（Ⅱ）設點的軌跡為曲線
，過點
的直線
交曲線于
，
兩點，過且與垂直的直線
交圓于
，兩點，求四邊形
面積的取值范圍.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖4，在四棱錐
中，
底面
，底面為直角梯形，
，過
作平面分別交線段
于點
.
（1）證明：
；
（2）若直線
與平面所成的線面角的正切值為
，則當點
在線段的何處時，直線
與平面
所成角為
？
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】設橢圓C：
的左、右焦點分別為
、
，上頂點為A，在x軸負半軸上有一點B，滿足為線段
的中點，且AB⊥
。
（I）求橢圓C的離心率；
（II）若過A、B、三點的圓與直線
：
相切，求橢圓C的方程；
（III）在（I）的條件下，過右焦點作斜率為k的直線與橢圓C交于M，N兩點，在x軸上是否存在點P(m，0)使得以PM，PN為鄰邊的平行四邊形是菱形？如果存在，求出m的取值范圍；如果不存在，說明理由。
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】（2017-2018學年安徽省六安市第一中學高三上學期第二次月考）已知函數
是偶函數.
(1)求
的值;
(2)若函數
的圖象與直線
沒有交點,求
的取值范圍;
(3)若函數
,是否存在實數
使得
的最小值為0,若存在,求出的值;若不存在,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
