
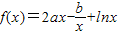 在x=1和
在x=1和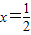 處取得極值.
處取得極值. 上存在x,使得不等式f(x)-c≤0成立,求實數c的最小值.(參考數據e2≈7.389,e3≈20.08)
上存在x,使得不等式f(x)-c≤0成立,求實數c的最小值.(參考數據e2≈7.389,e3≈20.08)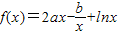 在x=1和
在x=1和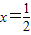 處取得極值,我們求出函數的導函數f′(x)的解析式,易得
處取得極值,我們求出函數的導函數f′(x)的解析式,易得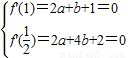 ,解方程組,即可得到實數a,b的值;
,解方程組,即可得到實數a,b的值;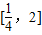 上存在x,使得不等式f(x)-c≤0成立,表示函數f(x)在區間
上存在x,使得不等式f(x)-c≤0成立,表示函數f(x)在區間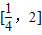 上的最小值小于等于c,根據(1)中函數的解析式,求出函數f(x)在區間
上的最小值小于等于c,根據(1)中函數的解析式,求出函數f(x)在區間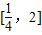 上的最小值,即可得到答案.
上的最小值,即可得到答案.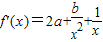 …(2分)
…(2分)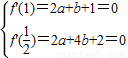 ,解得,
,解得,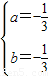
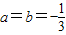 …(5分)
…(5分)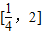 上存在x,使不等式f(x)-c≤0成立,只需c≥[f(x)]min
上存在x,使不等式f(x)-c≤0成立,只需c≥[f(x)]min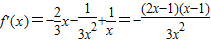
 時,f′(x)<0,故函數f(x)在
時,f′(x)<0,故函數f(x)在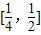 上單調遞減,
上單調遞減,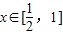 時,f′(x)>0,故函數f(x)在
時,f′(x)>0,故函數f(x)在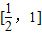 上單調遞增,
上單調遞增,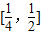 上單調遞減…(7分)
上單調遞減…(7分)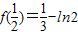 是f(x)在
是f(x)在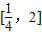 上的極小值,且函數f(x)的最小值必是
上的極小值,且函數f(x)的最小值必是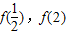 兩者中較小的…(8分)
兩者中較小的…(8分)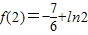 ,
,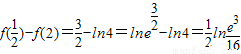 ∵e3≈20.08>16,
∵e3≈20.08>16, ∴
∴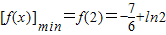 …(9分)∴
…(9分)∴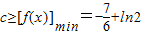
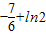 .…(10分)
.…(10分)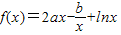 在x=1和
在x=1和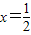 處取得極值,構造關于a,b的方程,確定出函數f(x)的解析式,是解答本題的關鍵.
處取得極值,構造關于a,b的方程,確定出函數f(x)的解析式,是解答本題的關鍵. 

科目:高中數學 來源: 題型:解答題
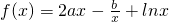 在x=1和
在x=1和 處取得極值.
處取得極值.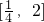 上存在x0,使得不等式f(x0)-c≤0成立,求實數c的最小值.(參考數據e2≈7.389,e3≈20.08)
上存在x0,使得不等式f(x0)-c≤0成立,求實數c的最小值.(參考數據e2≈7.389,e3≈20.08)查看答案和解析>>
科目:高中數學 來源:2009-2010學年吉林省長春市東北師大附中高二(上)期末數學試卷(理科)(解析版) 題型:解答題
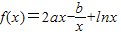 在x=1和
在x=1和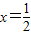 處取得極值.
處取得極值.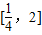 上存在x,使得不等式f(x)-c≤0成立,求實數c的最小值.(參考數據e2≈7.389,e3≈20.08)
上存在x,使得不等式f(x)-c≤0成立,求實數c的最小值.(參考數據e2≈7.389,e3≈20.08)查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com