
 的元素全為實數,且滿足:若
的元素全為實數,且滿足:若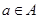 ,則
,則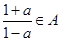 。
。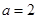 ,求出
,求出 中其它所有元素;
中其它所有元素; 中的元素?請你設計一個實數
中的元素?請你設計一個實數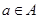 ,再求出
,再求出 中的所有元素?
中的所有元素? 中元素為
中元素為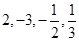 (2)
(2)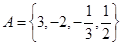 (3)A中的元素為4的倍數
(3)A中的元素為4的倍數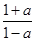
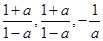 三式均有意義時,對a的限制,而不能得到滿分.
三式均有意義時,對a的限制,而不能得到滿分.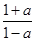 ∈A,
∈A,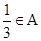 由a=2∈A,可得
由a=2∈A,可得 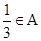 ,再由
,再由 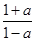 ∈A,令0∈A,可得-1∈A,根據此時
∈A,令0∈A,可得-1∈A,根據此時 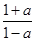 ∈A,結合(1)的結論可得
∈A,結合(1)的結論可得 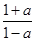 ∈A,而根據(2)的結論,可得要使 三式
∈A,而根據(2)的結論,可得要使 三式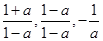 ,均有意義,應有a≠0,a≠±1
,均有意義,應有a≠0,a≠±1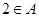 ,則
,則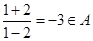 ,又由
,又由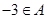 ,得
,得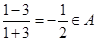 ,再由
,再由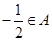
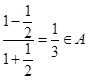 ,而
,而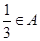 ,得
,得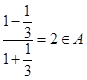 ,故
,故 中元素為
中元素為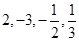 .… 4分
.… 4分 不是
不是 的元素.若
的元素.若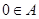 ,則
,則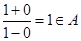 ,而當
,而當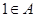 時,
時,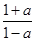 不存在,故0不是
不存在,故0不是 的元素.取
的元素.取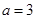 ,可得
,可得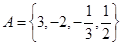 .……………… 8分
.……………… 8分 中沒有元素
中沒有元素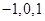 ;②已知A中的一個元素可得其余3個,且每兩個互為負倒數.③A中元素個數為4的倍數。………10分
;②已知A中的一個元素可得其余3個,且每兩個互為負倒數.③A中元素個數為4的倍數。………10分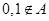 .若
.若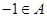 ,則
,則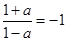 無解.故
無解.故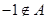 ……12分
……12分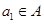 ,則
,則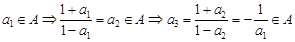
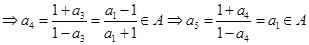 ,
,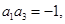
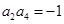 .
.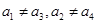 .若
.若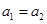 ,則
,則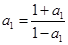 ,得:
,得: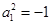 無實數解.
無實數解.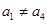 .
.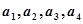 四個互不相等的數.
四個互不相等的數.

湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com