
對于函數 ,若存在
,若存在 ,使
,使 ,則稱
,則稱 是
是 的一
的一
個"不動點".已知二次函數
(1)當 時,求函數
時,求函數 的不動點;
的不動點;
(2)對任意實數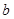 ,函數
,函數 恒有兩個相異的不動點,求
恒有兩個相異的不動點,求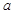 的取值范圍;
的取值范圍;
(3)在(2)的條件下,若 的圖象上
的圖象上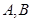 兩點的橫坐標是
兩點的橫坐標是 的不動點,
的不動點,
且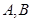 兩點關于直線
兩點關于直線 對稱,求
對稱,求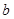 的最小值.
的最小值.
(1)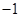 和
和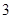 (2)
(2)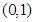 (3)
(3)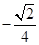
【解析】(1)將a、b代入函數,根據條件“若存在x0∈R,使f(x0)=x0成立,則稱x0為f(x)的不動點”建立方程解之即可;
(2)對任意實數b,f(x)恒有兩個相異不動點轉化成對任意實數b,ax2+(b+1)x+b-1=x恒有兩個不等實根,再利用判別式建立a、b的不等關系,最后將b看成變量,轉化成關于b的恒成立問題求解即可.
(3)在(2)的條件下,可得由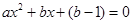 得
得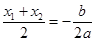 ,由題意知
,由題意知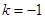 ,
,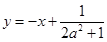 ,從而可確定AB的中點E的坐標
,從而可確定AB的中點E的坐標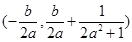 ,從而可得
,從而可得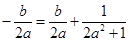 ,整理后得
,整理后得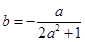 ,這樣就轉化為b關于a的函數問題來解決即可.
,這樣就轉化為b關于a的函數問題來解決即可.
解:(1)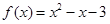 ,
,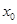 是
是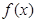 的不動點,則
的不動點,則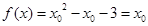 ,
,
得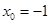 或
或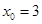 ,函數
,函數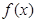 的不動點為
的不動點為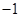 和
和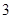 .……………… 3分
.……………… 3分
(2)∵函數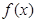 恒有兩個相異的不動點,∴
恒有兩個相異的不動點,∴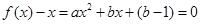 恒有兩
恒有兩
個不等的實根,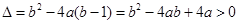 對
對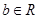 恒成立,
恒成立,
∴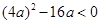 ,得
,得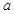 的取值范圍為
的取值范圍為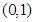 . …………7分
. …………7分
(3)由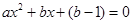 得
得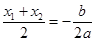 ,由題知
,由題知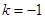 ,
,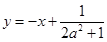 ,
,
設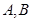 中點為
中點為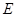 ,則
,則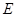 的橫坐標為
的橫坐標為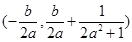 ,∴
,∴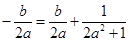 ,
,
∴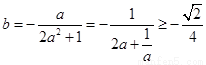 ,當且僅當
,當且僅當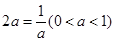 ,即
,即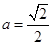 時等號
時等號
成立,
∴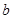 的最小值為
的最小值為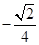 .………………………… 12分
.………………………… 12分


 名校課堂系列答案
名校課堂系列答案科目:高中數學 來源:2012屆湖南省漣源一中高三第四次月考理科數學試卷 題型:解答題
對于函數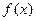 ,若存在
,若存在 ,使
,使 成立,則稱
成立,則稱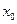 為
為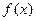 的不動點.如果函數
的不動點.如果函數 有且僅有兩個不動點0,2,且
有且僅有兩個不動點0,2,且 .
.
(1) 求函數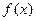 的單調區間;
的單調區間;
(2) 已知數列 各項不為零且不為1,滿足
各項不為零且不為1,滿足 ,求證:
,求證: ;
;
設 ,
, 為數列
為數列 的前
的前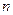 項和,求證:
項和,求證: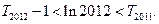
查看答案和解析>>
科目:高中數學 來源:2011-2012學年湖南省高三第四次月考理科數學試卷 題型:解答題
對于函數 ,若存在
,若存在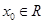 ,使
,使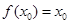 成立,則稱
成立,則稱 為
為 的不動點.如果函數
的不動點.如果函數 有且僅有兩個不動點0,2,且
有且僅有兩個不動點0,2,且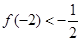 .
.
(1)
求函數 的單調區間;
的單調區間;
(2)
已知數列 各項不為零且不為1,滿足
各項不為零且不為1,滿足 ,求證:
,求證: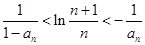 ;
;
設 ,
, 為數列
為數列 的前
的前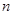 項和,求證:
項和,求證:
查看答案和解析>>
科目:高中數學 來源:2011-2012學年江西省高三第二次月考試卷理科數學 題型:解答題
(本小題滿分14分)對于函數 ,若存在
,若存在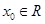 ,使
,使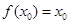 成立,則稱
成立,則稱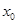 為
為 的不動點。如果函數
的不動點。如果函數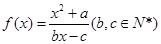 有且僅有兩個不動點
有且僅有兩個不動點 、
、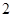 ,且
,且
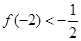 。
。
(1)試求函數 的單調區間;
的單調區間;
(2)已知各項均為負的數列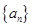 滿足
滿足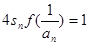 ,求證:
,求證: ;
;
(3)設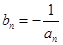 ,
,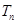 為數列
為數列 的前
的前 項和,求證:
項和,求證: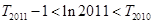 。
。
查看答案和解析>>
科目:高中數學 來源:云南省2010-2011學年高三數學一輪復習測試:函數(1) 題型:解答題
對于函數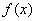 ,若存在
,若存在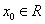 ,使
,使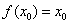 成立,則稱
成立,則稱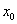 為
為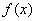 的不動點.如果函數
的不動點.如果函數 有且僅有兩個不動點
有且僅有兩個不動點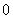 、
、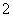 ,且
,且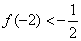 .試求函數
.試求函數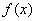 的單調區間;
的單調區間;
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com