
分析 (1)基本事件總數n=6×6=36,設事件A表示“f(x)=x2-2(a-2)x-b2+13=0有兩個不等正根“,利用列舉法求出滿足事件A的基本事件個數,由此能求出方程f(x)=0有兩個不等正根的概率.
(2)設事件B表示“函數f(x)在區間[2,3]上是單調函數”,a∈[2,6],f(x)=x2-2(a-2)x-b2+13的對稱軸為x=a-2∈[0,4],f(x)在區間[2,3]上為增函數時,只要對稱軸不在[2,3]上即可,根據幾何概型定義得函數f(x)在區間[2,3]上是單調函數的概率.
解答 解:(1)如果先后拋擲的一枚均勻的骰子所得的向上的點數記為(a,b),
則基本事件總數n=6×6=36,
設事件A表示“f(x)=x2-2(a-2)x-b2+13=0有兩個不等正根“,
則事件A滿足:$\left\{\begin{array}{l}{a-2>0}\\{13-{b}^{2}>0}\\{(a-2)^{2}+{b}^{2}-13>0}\end{array}\right.$,
滿足事件A的基本事件有:(5,3),(6,1),(6,2),(6,3),共有m=4個,
∴方程f(x)=0有兩個不等正根的概率p(A)=$\frac{m}{n}=\frac{4}{36}=\frac{1}{9}$.
(2)設事件B表示“函數f(x)在區間[2,3]上是單調函數”,
∵a∈[2,6],f(x)=x2-2(a-2)x-b2+13的對稱軸為x=a-2∈[0,4],
區間長為4,
f(x)在區間[2,3]上為增函數時,只要對稱軸不在[2,3]上即可,
∴對稱軸不在[2,3]的區間長為3,
根據幾何概型定義得函數f(x)在區間[2,3]上是單調函數的概率P(B)=$\frac{3}{4}$.
點評 本題考查分層抽樣、統計圖的應用,考查概率的求法,是中檔題,解題時要認真審題,注意列舉法和幾何概型的合理運用.


科目:高中數學 來源: 題型:解答題
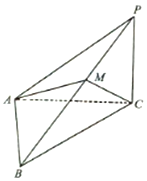 如圖,在三棱錐P-ABC中,PC⊥平面ABC,∠PAC=30°,∠ACB=45°,BC=2$\sqrt{2}$,PA⊥AB.
如圖,在三棱錐P-ABC中,PC⊥平面ABC,∠PAC=30°,∠ACB=45°,BC=2$\sqrt{2}$,PA⊥AB.查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | ① | B. | ② | C. | ③ | D. | ④ |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
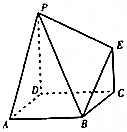 如圖,多面體ABCDPE的底面ABCD是平行四邊形,AD=AB=2,$\overrightarrow{AB}$•$\overrightarrow{AD}$=0,PD⊥平面ABCD,EC∥PD,且PD=2EC=2,則二面角A-PB-E的大小為( )
如圖,多面體ABCDPE的底面ABCD是平行四邊形,AD=AB=2,$\overrightarrow{AB}$•$\overrightarrow{AD}$=0,PD⊥平面ABCD,EC∥PD,且PD=2EC=2,則二面角A-PB-E的大小為( )| A. | $\frac{2π}{3}$ | B. | $\frac{π}{6}$ | C. | $\frac{π}{3}$ | D. | $\frac{5π}{6}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 96 | B. | 192 | C. | 95 | D. | 190 |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com