
【題目】在平面直角坐標系中,![]() ,
,![]() ,
,![]() (O是坐標原點),其中
(O是坐標原點),其中![]() 。
。
(1)求B點坐標;
(2)求四邊形OABC在第一象限部分面積![]() .
.
【答案】(1)![]() .
.
(2)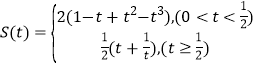 .
.
【解析】
分析:(1)利用向量的加法運算,表示出![]() ,再根據OABC為矩形的特征,表示出B點坐標。
,再根據OABC為矩形的特征,表示出B點坐標。
(2)討論當t取不同值時(也就是B點坐標在第一象限或第二象限),四邊形OABC落在第一象限內的面積。當點B在第一象限時,落在第一象限內的部分為直角梯形,可用整個面積減去第二象限面積的方法求得;當B在第二象限時,落在第一象限內的部分為直角三角形,可以直接求得。最后結果寫成分段函數的形式。
詳解:(1)∵![]() ,
,
∴![]() 為平行四邊形,
為平行四邊形,
又∵![]() ,∴
,∴![]() ,
,
∴![]() 為矩形,
為矩形,
∵![]() ,
,
∴![]()
(2)①當![]() ,即
,即![]() 時,
時,![]() 在第一象限,
在第一象限,![]() 在第一象限,
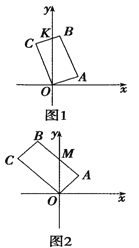
在第一象限,![]() 在第二象限(如圖1),此時
在第二象限(如圖1),此時![]() 的方程為
的方程為![]() ,令
,令![]() ,得
,得![]() 交
交![]() 軸于
軸于![]()
![]() ,
,
∴![]()
②當![]() ,即
,即![]() 時,
時,![]() 在第一象限,
在第一象限,![]() 在
在![]() 軸上或在第二象限,
軸上或在第二象限,![]() 在第二象限(如圖2),此時
在第二象限(如圖2),此時![]() 的方程為
的方程為![]() ,令
,令![]() ,得
,得![]() 交
交![]() 軸于
軸于![]() ,
,
∴![]() ,
,
∴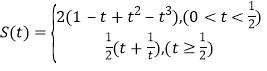 .
.


 作業輔導系列答案
作業輔導系列答案科目:高中數學 來源: 題型:
【題目】已知拋物線 ![]() 的焦點為
的焦點為 ![]() ,
, ![]() 是拋物線上橫坐標為4,且位于
是拋物線上橫坐標為4,且位于 ![]() 軸上方的點,
軸上方的點, ![]() 到拋物線準線的距離等于5,過
到拋物線準線的距離等于5,過 ![]() 作
作 ![]() 垂直于
垂直于 ![]() 軸,垂足為
軸,垂足為 ![]() ,
, ![]() 的中點為
的中點為 ![]() .
.
(1)求拋物線的方程;
(2)若過 ![]() 作
作 ![]() ,垂足為
,垂足為 ![]() ,求點
,求點 ![]() 的坐標.
的坐標.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某工廠生產某種產品,每生產1噸產品需人工費4萬元,每天還需固定成本3萬元.經過長期調查統計,每日的銷售額![]() (單位:萬元)與日產量
(單位:萬元)與日產量![]() (單位:噸)滿足函數關系
(單位:噸)滿足函數關系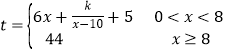 ,已知每天生產4噸時利潤為7萬元.
,已知每天生產4噸時利潤為7萬元.
(1)求![]() 的值;
的值;
(2)當日產量為多少噸時,每天的利潤最大,最大利潤為多少?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓 ![]() 的右焦點為
的右焦點為 ![]() ,上頂點為
,上頂點為 ![]() ,
, ![]() 周長為
周長為 ![]() ,離心率為
,離心率為 ![]() .
.
(1)求橢圓 ![]() 的方程;
的方程;
(2)若點 ![]() 是橢圓
是橢圓 ![]() 上第一象限內的一個點,直線
上第一象限內的一個點,直線 ![]() 過點
過點 ![]() 且與直線
且與直線 ![]() 平行,直線
平行,直線 ![]() 且
且 ![]() 與橢圓
與橢圓 ![]() 交于
交于 ![]() 兩點,與
兩點,與 ![]() 交于點
交于點 ![]() ,是否存在常數
,是否存在常數 ![]() ,使
,使 ![]() .若存在,求出
.若存在,求出 ![]() 的值,若不存在,請說明理由.
的值,若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某保險公司有一款保險產品的歷史收益率(收益率=利潤÷保費收入)的頻率分布直方圖如圖所示:
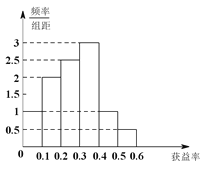
(Ⅰ)試估計平均收益率;
(Ⅱ)根據經驗,若每份保單的保費在20元的基礎上每增加![]() 元,對應的銷量
元,對應的銷量![]() (萬份)與
(萬份)與![]() (元)有較強線性相關關系,從歷史銷售記錄中抽樣得到如下5組
(元)有較強線性相關關系,從歷史銷售記錄中抽樣得到如下5組![]() 與
與![]() 的對應數據:
的對應數據:

據此計算出的回歸方程為![]() .
.
(i)求參數![]() 的估計值;
的估計值;
(ii)若把回歸方程![]() 當作
當作![]() 與
與![]() 的線性關系,用(Ⅰ)中求出的平均收益率估計此產品的收益率,每份保單的保費定為多少元時此產品可獲得最大收益,并求出該最大收益.
的線性關系,用(Ⅰ)中求出的平均收益率估計此產品的收益率,每份保單的保費定為多少元時此產品可獲得最大收益,并求出該最大收益.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】潮州統計局就某地居民的月收入調查了![]() 人,并根據所得數據畫了樣本的頻率分
人,并根據所得數據畫了樣本的頻率分
布直方圖(每個分組包括左端點,不包括右端點,如第一組表示收入在![]() )。
)。

(1)求居民月收入在![]() 的頻率;
的頻率;
(2)根據頻率分布直方圖算出樣本數據的中位數;
(3)為了分析居民的收入與年齡、職業等方面的關系,必須按月收入再從這![]() 人中分層抽樣方法抽出
人中分層抽樣方法抽出![]() 人作進一步分析,則月收入在
人作進一步分析,則月收入在![]() 的這段應抽多少人?
的這段應抽多少人?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列說法正確的是( )
A.![]() ,y
,y ![]() R,若x+y
R,若x+y ![]() 0,則x
0,則x ![]() 且y
且y ![]()
B.a ![]() R,“
R,“ ![]() ”是“a>1”的必要不充分條件
”是“a>1”的必要不充分條件
C.命題“ ![]() x
x ![]() R,使得
R,使得 ![]() ”的否定是“
”的否定是“ ![]() R,都有
R,都有 ![]() ”
”
D.“若 ![]() ,則a<b”的逆命題為真命題
,則a<b”的逆命題為真命題
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知在△ABC中,角A,B,C所對的邊分別是a,b,c,且a、b、c成等比數列,c= ![]() bsinC﹣ccosB.
bsinC﹣ccosB.
(Ⅰ)求B的大小;
(Ⅱ)若b=2 ![]() ,求△ABC的周長和面積.
,求△ABC的周長和面積.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com