
分析 (1)判斷函數的奇偶性,利用奇偶性的定義證明即可.
(2)①利用函數的單調性的定義證明即可.②集合函數的單調性,寫出單調區間即可.
解答 解:(1)函數f(x)=x+$\frac{a}{x}$是奇函數…(1分)
函數f(x)=x+$\frac{a}{x}$的定義域為(-∞,0)∪(0,+∞),關于原點對稱…(2分)
且f(-x)=-x-$\frac{a}{x}$=-(x+$\frac{a}{x}$)=-f(x)…(3分)
∴f(x)是奇函數…(4分)
(2)?①任取x1,x2∈(0,+∞)且x1<x2,
則$f({x_2})-f({x_1})={x_2}+\frac{4}{x_2}-{x_1}-\frac{4}{x_1}=({x_2}-{x_1})+\frac{{4({x_1}-{x_2})}}{{{x_1}{x_2}}}$=$({x_2}-{x_1})(1-\frac{4}{{{x_1}{x_2}}})=\frac{{({x_2}-{x_1})({x_1}{x_2}-4)}}{{{x_1}{x_2}}}$…(6分)
當0<x1<x2<2時,x2-x1>0,x1x2>0
∴f(x2)-f(x1)<0,即f(x1)>f(x2).∴f(x)在(0,2)上單調遞減;…(8分)
當2<x1<x2時,x2-x1>0,x1x2-4>0,x1x2>0∴f(x2)-f(x1)>0,即f(x1)<f(x2).∴f(x)在(2,+∞)上單調遞增;…(10分)
②?∵f(x)Z是奇函數,f(x)在(0,2)上單調遞減,在(2,+∞)上單調遞增,
∴f(x)在(-2,0)上單調遞減,在(-∞,-2)上單調遞增;…(12分)
點評 本題考查函數的奇偶性以及函數的單調性的判斷與應用,考查轉化思想以及計算能力.


 沖刺100分1號卷系列答案
沖刺100分1號卷系列答案科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | -12 | B. | 6 | C. | -6 | D. | 32 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | (-1,1] | B. | [-1,1] | C. | (-∞,1] | D. | [-1,+∞) |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | -$\frac{\sqrt{3}}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | -1 | D. | 1 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
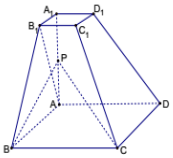 已知四棱臺ABCD-A1B1C1D1的上下底面分別是邊長為2和4的正方形,AA1=4且AA1⊥底面ABCD,點P為AA1的中點.
已知四棱臺ABCD-A1B1C1D1的上下底面分別是邊長為2和4的正方形,AA1=4且AA1⊥底面ABCD,點P為AA1的中點.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com