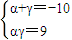(1)求證,若方程x3+ax2+bx+c=0的三根可排成等比數列,則a3c=b3.
(2)已知方程x3+7x2-21x-27=0的三根可以排成等比數列,求三根.
【答案】
分析:(1)設出原方程的三根,根據一元三次方程根與系數的關系得到三根的三個關系式,又三根可排成等比數列,根據等比數列的性質得到中間的一根的平方等于其他兩根的積即β
2=αγ,要證a
3c=b
3即要證
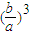
=c,把a與b代入等號的左邊,化簡后得到c,得證;
(2)根據(1)可知β
3=-c,又由方程得到c=-27,進而求出β的值,由三根之和等于-7,得到其他兩根之和,記作①,由三根成等比數列得到β
2=αγ,將β的值代入即可求出其他兩根之積,記作②,聯立①②即可求出其他的兩個根,依次寫出三根即可.
解答:解:(1)設α,β,γ是方程x
3+ax
2+bx+c=0的三根,
由根與系數關系可知:α+β+γ=-a,αβ+βγ+γα=b,αβγ=-c,
又因α,β,γ排成等比數列,于是β
2=αγ.
則
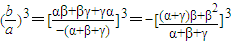
=
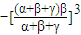
=-β
3=-αβγ=c
即a
3c=b
3,得證;
(2)解:由(1)可知β
3=-c,∴β
3=27,
∴β=3.代入α+β+γ=-7
可得α+γ=-10,又由α,β,γ成等比數列,∴β
2=αγ,
即αγ=9,故可得方程組:
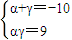
解之,可得α=-9或-1,γ=-1或-9.
于是,所求之三根為-9,3,-1或-1,3,-9.
點評:此題考查學生掌握一元n次方程的根與系數的關系,靈活運用等比數列的性質化簡求值,是一道中檔題.

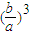 =c,把a與b代入等號的左邊,化簡后得到c,得證;
=c,把a與b代入等號的左邊,化簡后得到c,得證;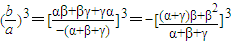
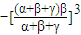 =-β3=-αβγ=c
=-β3=-αβγ=c