
設f(x)=lnx+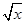 -1,證明:
-1,證明:
(1)當x>1時,f(x)< 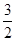 (x-1);
(x-1);
(2)當1<x<3時,f(x)< 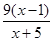 .
.
(1)見解析(2)見解析
【解析】證明:(1)(證法一)記g(x)=lnx+ -1-
-1-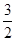 (x-1).則當x>1時,
(x-1).則當x>1時,
g′(x)=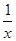 +
+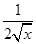 -
-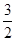 <0,g(x)在(1,+∞)上單調遞減.
<0,g(x)在(1,+∞)上單調遞減.
又g(1)=0,有g(x)<0,即f(x)< 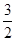 (x-1).
(x-1).
(證法二)
由均值不等式,當x>1時,2  <x+1,故
<x+1,故 <
< 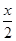 +
+ .①
.①
令k(x)=lnx-x+1,則k(1)=0,k′(x)=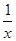 -1<0,
-1<0,
故k(x)<0,即lnx<x-1.②
由①②得,當x>1時,f(x)< 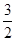 (x-1).
(x-1).
(2)(證法一)記h(x)=f(x)-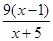 ,由(1)得
,由(1)得
h′(x)=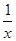 +
+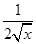 -
-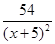 =
=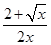 -
-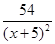 <
< 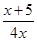 -
-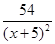 =
=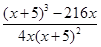 .
.
令g(x)=(x+5)3-216x,則當1<x<3時,g′(x)=3(x+5)2-216<0.
因此g(x)在(1,3)內是遞減函數,又由g(1)=0,得g(x)<0,所以h′(x)<0.
因此h(x)在(1,3)內是遞減函數,又由h(1)=0,得h(x)<0.于是當1<x<3時,f(x)< 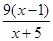 .
.
(證法二)記h(x)=(x+5)f(x)-9(x-1),
則當1<x<3時,由(1)得h′(x)=f(x)+(x+5)f′(x)-9< 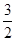 (x-1)+(x+5)
(x-1)+(x+5)  -9
-9
= [3x(x-1)+(x+5)(2+
[3x(x-1)+(x+5)(2+ )-18x]<
)-18x]< 
=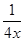 (7x2-32x+25)<0.
(7x2-32x+25)<0.
因此h(x)在(1,3)內單調遞減,又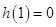 ,所以
,所以 ,即
,即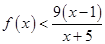 .
.


科目:高中數學 來源: 題型:013
設F(x)=lnx,f(x)=1-x2,則函數g(x)=F[f(x)]的定義域是( )
A.(0,+∞) B.(-∞,+∞)
C.{x|x∈R且x≠±1} D.(-1,1)
查看答案和解析>>
科目:高中數學 來源:數學教研室 題型:013
A.(0,+∞) B.(-∞,+∞)
C.{x|x∈R且x≠±1} D.(-1,1)
查看答案和解析>>
科目:高中數學 來源:浙江省上虞市2007-2008學年度高三第一學期期中測試數學試卷 題型:044
設f(x)=lnx-![]() (x≥1),g(x)=2(x-1)-(x2+1)lnx(x≥1).
(x≥1),g(x)=2(x-1)-(x2+1)lnx(x≥1).
(1)求證f(x)和g(x)在[1,+∞)上均為減函數;
(2)設b>1,證明不等式![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
(05年湖南卷理)(14分)
已知函數f(x)=lnx,g(x)=![]() ax2+bx,a≠0.
ax2+bx,a≠0.
(Ⅰ)若b=2,且h(x)=f(x)-g(x)存在單調遞減區間,求a的取值范圍;
(Ⅱ)設函數f(x)的圖象C1與函數g(x)圖象C2交于點P、Q,過線段PQ的中點作x軸的垂線分別交C1,C2于點M、N,證明C1在點M處的切線與C2在點N處的切線不平行.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com