
(13分)已知函數f(x)=ax+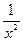 (x≠0,常數a∈R).
(x≠0,常數a∈R).
(1)討論函數f(x)的奇偶性,并說明理由;
(2)若函數f(x)在x∈[3,+∞)上為增函數,求a的取值范圍.
解:(1)定義域(-∞,0)∪(0,+∞),關于原點對稱.
當a=0時,f(x)=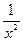 ,滿足對定義域上任意x,f(-x)=f(x),
,滿足對定義域上任意x,f(-x)=f(x),
∴a=0時,f(x)是偶函數;
當a≠0時,f(1)=a+1,f(-1)=1-a,
若f(x)為偶函數,則a+1=1-a,a=0矛盾;
若f(x)為奇函數,則1-a=-(a+1),1=-1矛盾,∴當a≠0時,f(x)是非奇非偶函數.
(2)任取x1>x2≥3,f(x1)-f(x2)=ax1+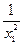 -ax2-
-ax2-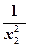
=a(x1-x2)+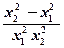 =(x1-x2)(a-
=(x1-x2)(a-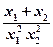 ).
).
∵x1-x2>0,f(x)在[3,+∞)上為增函數,
∴a>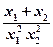 ,即a>
,即a>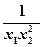 +
+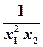 在[3,+∞)上恒成立.
在[3,+∞)上恒成立.
∵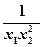 +
+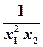 <
<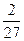 ,∴a≥
,∴a≥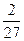 .
.
解析


科目:高中數學 來源: 題型:解答題
(12分 ) .已知函數y=
) .已知函數y= f(x)=
f(x)=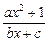 (a,b,c∈R,a>0,b>0)是奇函數,當x>0時,f(x)有最小值2,其中b∈N且f(1)<
(a,b,c∈R,a>0,b>0)是奇函數,當x>0時,f(x)有最小值2,其中b∈N且f(1)<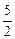
(1)試求函數f(x)的解析式
(2)問函數f(x)圖象上是否存在關于點(1,0)對稱的兩點,若存在,求出點的坐標;若不存在,說 明理由.
明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某民營企業生產A,B兩種產品,根據市場調查和預測,A產品的利潤與投資成正比,其關系如圖1,B產品的利潤與投資的算術平方根成正比,其關系如圖2(注:利潤與投資單位是萬元)
(1)分別將A,B兩種產品的利潤表示為投資的函數,并寫出它們的函數關系式。
(2)該企業已籌集到10萬元資金,并全部投入A,B兩種產品的生產,問:怎樣分配這10萬元投資,才能是企業獲得最大利潤,其最大利潤約為多少萬元。( 精確到1萬元)。
精確到1萬元)。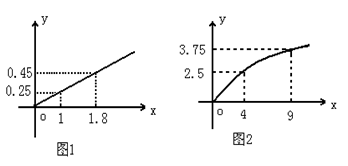
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
(本小題滿分12分)
(文科)已知二次函數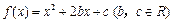 ,且
,且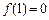 .
.
(1)若函數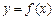 與x軸的兩個交點
與x軸的兩個交點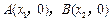 之間的距離為2,求b的值;
之間的距離為2,求b的值;
(2)若關于x的方程 的兩個實數根分別在區間
的兩個實數根分別在區間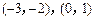 內,求b的取值范圍.
內,求b的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
(本小題滿分12分)定義在R上的奇函數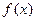 有最小正周期4,且
有最小正周期4,且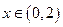 時,
時,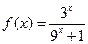 。
。
⑴求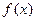 在
在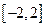 上的解析式;
上的解析式;
⑵判斷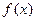 在
在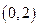 上的單調性,并給予證明;
上的單調性,并給予證明;
⑶當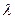 為何值時,關于方程
為何值時,關于方程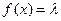 在
在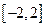 上有實數解?
上有實數解?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com