
(10分)
某酒廠有甲、乙兩條生產線生產同一種型號的白酒。產品在自動傳輸帶上包裝傳送,每15分鐘抽一瓶測定其質量是否合格,分別記錄抽查的數據如下(單位:毫升):
甲生產線:508, 504, 496, 510, 492, 496
乙生產線:515, 520, 480, 485, 497, 503
問:(1) 這種抽樣是何種抽樣方法?
(2)分別計算甲、乙兩條生產線的平均值與方差,并說明哪條生產線的產品較穩定。
 名校課堂系列答案
名校課堂系列答案科目:高中數學 來源: 題型:解答題
從甲、乙兩名運動員的若干次訓練成績中隨機抽取6次,分別為
甲:7.7,7.8,8.1,8.6,9.3,9.5
乙:7.6,8.0,8.2,8.5,9.2,9.5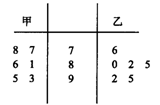
(1)根據以上的莖葉圖,對甲、乙運動員的成績作比較,寫出兩個統計結論;
(2)從甲、乙運動員六次成績中各隨機抽取1次成績,求甲、乙運動員的成績至少有一個高于8.5分的概率。
(3)經過對甲、乙運動員若干次成績進行統計,發現甲運動員成績均勻分布在[7.5,9.5]之間,乙運動員成績均勻分布在[7.0,10]之間,現甲、乙比賽一次,求甲、乙成績之差的絕對值小于0.5分的概率。
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
(本小題滿分12分)
我國是世界上嚴重缺水的國家之一,城市缺水問題較為突出.某市政府為了節約生活用水,計劃在本市試行居民生活用水定額管理,為此市政府首先采用抽樣調查的方法獲得了 位居民某年的月均用水量(單位:噸).根據所得的
位居民某年的月均用水量(單位:噸).根據所得的 個數據按照區間
個數據按照區間 進行分組,得到頻率分布直方圖如圖
進行分組,得到頻率分布直方圖如圖
(1)若已知 位居民中月均用水量小于1噸的人數是12,求
位居民中月均用水量小于1噸的人數是12,求 位居民中月均用水量分別在區間
位居民中月均用水量分別在區間 和
和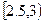 內的人數;
內的人數;
(2)在該市居民中隨意抽取10位,求至少有2位居民月均用水量在區間 或
或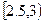 內的概率.(精確到0.01.參考數據:
內的概率.(精確到0.01.參考數據: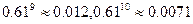 )
)
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
(本小題滿分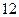 分)
分)
為了解某市的交通狀況,現對其6條道路進行評估,得分分別為:5,6,7,8,9,10.
規定評估的平均得分與全市的總體交通狀況等級如下表:
(1)求本次評估的平均得分,并參照上表估計該市的總體交通狀況等級;
(2)用簡單隨機抽樣方法從這 條道路中抽取
條道路中抽取 條,它們的得分組成一個樣本,求該樣本的平均數與總體的平均數之差的
條,它們的得分組成一個樣本,求該樣本的平均數與總體的平均數之差的 絕對值不超過
絕對值不超過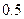 的概率.
的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
(本題滿分14分)
為了解高中一年級學生身高情況,某校按10%的比例對全校700名高中一年級學生按性別
進行抽樣檢查,測得身高頻數分布表如下表1、表2. 表1:男生身高頻數分布表
表1:男生身高頻數分布表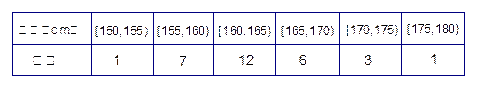 表2:女生身高頻數分布表
表2:女生身高頻數分布表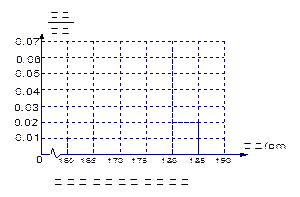 (1)求該校男生的人數并完成下面頻率分布直方圖;
(1)求該校男生的人數并完成下面頻率分布直方圖;
(2)估計該校學生身高(單位:cm)在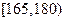 的概率;
的概率;
(3)在男生樣本中,從身高(單位:cm)在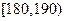 的男生中任選3人,設
的男生中任選3人,設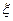 表示所選3人中身高(單位:cm)在
表示所選3人中身高(單位:cm)在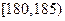 的人數,求
的人數,求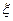 的分布列和數學期望.
的分布列和數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某班50名學生在一次數學測試中,成績全部介于50與100之間,將測試結果按如下方式分成五組:第一組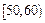 ,第二組
,第二組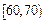 ,…,第五組
,…,第五組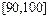 .下圖是按上述分組方法得到的頻率分布直方圖。
.下圖是按上述分組方法得到的頻率分布直方圖。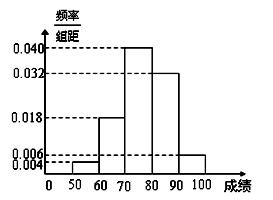
(Ⅰ)若成績大于或等于60且小于80,認為合格,求該班在這次數學測試中成績
合格的人數;
(Ⅱ)從測試成績在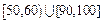 內的所有
內的所有
學生中隨機抽取兩名同學,設其測試成績分別為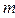 ,
,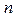 ,求事件“
,求事件“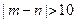 ”概率.
”概率.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
(本小題12分)
已知某商品的價格 (元)與需求量
(元)與需求量 (件)之間的關系有如下一組數據:
(件)之間的關系有如下一組數據:
 | 14 | 16 | 18 | 20 | 22 |
 | 12 | 10 | 7 | 5 | 3 |
 關于
關于 的散點圖
的散點圖 的值,并說明回歸模型擬合程度的好壞。
的值,并說明回歸模型擬合程度的好壞。查看答案和解析>>
科目:高中數學 來源: 題型:解答題
(本題滿分12分)
某幼兒園根據部分同年齡段女童的身高數據繪制了頻率分布直方圖, 其中身高的變化范圍是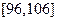 (單位:厘米),樣本數據分組為
(單位:厘米),樣本數據分組為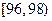 ,
,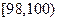 ,
,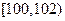 ,
,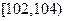 ,
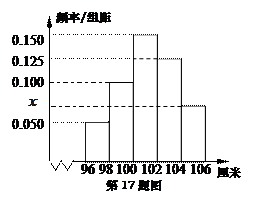
, ,
,
(Ⅰ)求出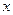 的值;
的值;
(Ⅱ)已知樣本中身高小于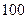 厘米的人數是
厘米的人數是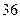 ,求出樣本總量
,求出樣本總量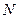 的數值;
的數值;
(Ⅲ)根據頻率分布直方圖提供的數據,求出樣本中身高大于或等于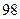 厘米并且小于
厘米并且小于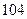 厘米學生數.
厘米學生數.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
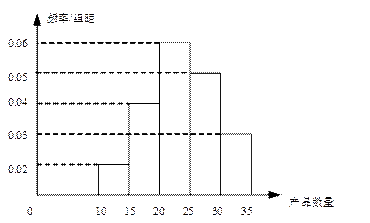
為了調查某廠2000名工人生產某種產品的能力,隨機抽查了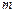 位工人某天生產該產品的數量,產品數量的分組區間為
位工人某天生產該產品的數量,產品數量的分組區間為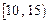 ,
, ,
,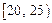 ,
,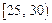 ,
,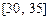 ,頻率分布直方圖如圖所示.已知生產的產品數量在
,頻率分布直方圖如圖所示.已知生產的產品數量在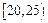 之間的工人有6位.
之間的工人有6位.
⑴求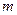 ;
;
⑵工廠規定從各組中任選1人進行再培訓,則選取5人不在同一組的概率是多少?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com