
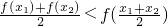 恒成立;
恒成立; 恒成立.
恒成立. ,
,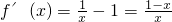 .
.
 =
= ,
, .
. ,
, .
. 恒成立,
恒成立, 對任意x1,x2∈(0,1)且x1≠x2恒成立,所以
對任意x1,x2∈(0,1)且x1≠x2恒成立,所以 .
. .
. ?
? ,
, .若f(x)滿足性質②,則
.若f(x)滿足性質②,則 恒成立.
恒成立. 對任意x1,x2∈(1,+∞)且x1≠x2恒成立,所以a
對任意x1,x2∈(1,+∞)且x1≠x2恒成立,所以a .
. .
. =
= ,由(Ⅰ)中的結論可得對任意x∈(0,1)∪(1,+∞),lnx<x-1(*)恒成立.(ⅰ)如果x1,x2∈(0,1),且x1≠x2,則
,由(Ⅰ)中的結論可得對任意x∈(0,1)∪(1,+∞),lnx<x-1(*)恒成立.(ⅰ)如果x1,x2∈(0,1),且x1≠x2,則 .根據(*)可得
.根據(*)可得 ,
, .由性質①轉化為恒成立問題,可得a的范圍;(ⅱ)如果x1,x2∈(1,+∞)且x1≠x2,則
.由性質①轉化為恒成立問題,可得a的范圍;(ⅱ)如果x1,x2∈(1,+∞)且x1≠x2,則 .再根據(*)進行放縮,由性質②可得恒成立問題,由此可得a的范圍,綜合(i)(ii)可得a的范圍;
.再根據(*)進行放縮,由性質②可得恒成立問題,由此可得a的范圍,綜合(i)(ii)可得a的范圍;

科目:高中數學 來源: 題型:
| e | 2 |
查看答案和解析>>
科目:高中數學 來源: 題型:
| 2x |
| x+2 |
| 9 |
| 10 |
| 1 |
| e2 |
查看答案和解析>>
科目:高中數學 來源: 題型:
| 5 | x+1 |
查看答案和解析>>
科目:高中數學 來源: 題型:
| 2 |
| 3 |
| 2 |
| x |
| 3 |
| 2 |
| 1 |
| 4 |
查看答案和解析>>
科目:高中數學 來源: 題型:
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com