
分析 (1)只要證明bn+1-bn=$\frac{1}{2{a}_{n+1}-1}$-$\frac{1}{2{a}_{n}-1}$=$\frac{1}{2-\frac{1}{2{a}_{n}}-1}$-$\frac{1}{2{a}_{n}-1}$,為常數.
(2)由(1)可得:bn=n.cn=bn+1•($\frac{1}{3}$)${\;}^{{b}_{n}}$=(n+1)$•(\frac{1}{3})^{n}$.利用“錯位相減法”與等比數列的求和公式即可得出.
(3)1+$\frac{1}{\sqrt{{b}_{2}}}$+$\frac{1}{\sqrt{{b}_{3}}}$+…+$\frac{1}{\sqrt{{b}_{n}}}$≤2$\sqrt{n}$-1(n∈N*)即為:1+$\frac{1}{\sqrt{2}}$+$\frac{1}{\sqrt{3}}$+…+$\frac{1}{\sqrt{n}}$≤$2\sqrt{n}$-1.由于$\frac{1}{\sqrt{k}}$=$\frac{2}{2\sqrt{k}}$<$\frac{2}{\sqrt{k-1}+\sqrt{k}}$=2$(\sqrt{k}-\sqrt{k-1})$(k=2,3,…).利用“裂項求和方法”即可得出.
解答 (1)證明:bn+1-bn=$\frac{1}{2{a}_{n+1}-1}$-$\frac{1}{2{a}_{n}-1}$=$\frac{1}{2-\frac{1}{2{a}_{n}}-1}$-$\frac{1}{2{a}_{n}-1}$=1,又b1=1.∴數列{bn}為等差數列,首項為1,公差為1.
(2)解:由(1)可得:bn=n.
cn=bn+1•($\frac{1}{3}$)${\;}^{{b}_{n}}$=(n+1)$•(\frac{1}{3})^{n}$.
∴數列{cn}的前n項和為Tn=$2×\frac{1}{3}$+3×$(\frac{1}{3})^{2}$+$4×(\frac{1}{3})^{3}$+…+(n+1)$•(\frac{1}{3})^{n}$.
$\frac{1}{3}{T}_{n}$=$2×(\frac{1}{3})^{2}$+3×$(\frac{1}{3})^{3}$+…+n$•(\frac{1}{3})^{n}$+(n+1)$•(\frac{1}{3})^{n+1}$,
∴$\frac{2}{3}$Tn=$2×\frac{1}{3}$+$(\frac{1}{3})^{2}$+$(\frac{1}{3})^{3}$+…+$(\frac{1}{3})^{n}$-(n+1)$•(\frac{1}{3})^{n+1}$=$\frac{1}{3}$+$\frac{\frac{1}{3}(1-\frac{1}{{3}^{n}})}{1-\frac{1}{3}}$-(n+1)$•(\frac{1}{3})^{n+1}$,
可得Tn=$\frac{5}{4}$-$\frac{2n+5}{4}×\frac{1}{{3}^{n}}$.
(3)證明:1+$\frac{1}{\sqrt{{b}_{2}}}$+$\frac{1}{\sqrt{{b}_{3}}}$+…+$\frac{1}{\sqrt{{b}_{n}}}$≤2$\sqrt{n}$-1(n∈N*)即為:1+$\frac{1}{\sqrt{2}}$+$\frac{1}{\sqrt{3}}$+…+$\frac{1}{\sqrt{n}}$≤$2\sqrt{n}$-1.
∵$\frac{1}{\sqrt{k}}$=$\frac{2}{2\sqrt{k}}$<$\frac{2}{\sqrt{k-1}+\sqrt{k}}$=2$(\sqrt{k}-\sqrt{k-1})$(k=2,3,…).
∴1+$\frac{1}{\sqrt{2}}$+$\frac{1}{\sqrt{3}}$+…+$\frac{1}{\sqrt{n}}$≤1+2[($\sqrt{2}$-1)+($\sqrt{3}-\sqrt{2}$)+…+($\sqrt{n}$-$\sqrt{n-1}$)]=1+2$(\sqrt{n}-1)$=2$\sqrt{n}$-1.
∴1+$\frac{1}{\sqrt{{b}_{2}}}$+$\frac{1}{\sqrt{{b}_{3}}}$+…+$\frac{1}{\sqrt{{b}_{n}}}$≤2$\sqrt{n}$-1(n∈N*).
點評 本題考查了“錯位相減法”、等比數列與等差數列的通項公式與求和公式、“裂項求和”方法、放縮法,考查了推理能力與計算能力,屬于難題.


 鴻圖圖書寒假作業假期作業吉林大學出版社系列答案
鴻圖圖書寒假作業假期作業吉林大學出版社系列答案科目:高中數學 來源: 題型:解答題
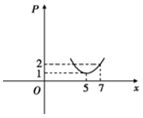 某產品關稅與市場供應量P的關系近似地滿足:P(x)=2${\;}^{(1-kt){{(x-b)}{\;}^2}}}$(其中t為關稅的稅率,且t∈[0,$\frac{1}{2}}$],x為市場價格,b,k為正常數),當t=$\frac{1}{8}$時,市場供應量曲線如圖所示:
某產品關稅與市場供應量P的關系近似地滿足:P(x)=2${\;}^{(1-kt){{(x-b)}{\;}^2}}}$(其中t為關稅的稅率,且t∈[0,$\frac{1}{2}}$],x為市場價格,b,k為正常數),當t=$\frac{1}{8}$時,市場供應量曲線如圖所示:查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | f($\frac{7}{2}$)<f(1)<f($\frac{5}{2}$) | B. | f(1)<f($\frac{5}{2}$)<f($\frac{7}{2}$) | C. | f($\frac{7}{2}$)<f($\frac{5}{2}$)<f(1) | D. | f($\frac{5}{2}$)<f(1)<f($\frac{7}{2}$) |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com