解:∵

=(

cosωx,sinωx),

=(sinωx,0),
∴

+

=(

cosωx+sinωx,sinωx).
故f(x)=(

+

)•

+k=

sinωxcosωx+sin
2ωx+k
=

sin2ωx+
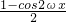
+k=

sin2ωx-

cos2ωx+

+k
=sin(2ωx-

)+k+

.
(1)由題意可知

=
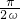
≥

,∴ω≤1.
又ω>0,∴0<ω≤1.
(2)∵T=

=π,∴ω=1.
∴f(x)=sin(2x-

)+k+

.
∵x∈[-

,

],∴2x-

∈[-

,

].
從而當2x-

=

,即x=

時,f(x)
max=f(

)=sin

+k+

=k+1=

,
∴k=-

.故f(x)=sin(2x-

).
由函數y=sinx的圖象向右平移

個單位長度,得到函數y=sin(x-

)的圖象,再將得到的函數圖象上所有點的橫坐標變為原來的

倍(縱坐標不變),得到函數y=sin(2x-

)的圖象.
分析:利用向量的數量積,化簡函數的表達式,通過二倍角、兩角差的正弦函數化簡函數為一個角的一個三角函數的形式,
(1)利用周期與函數f(x)的圖象中相鄰兩條對稱軸間的距離不小于

,得到關系式,求出ω的取值范圍;
(2)通過周期求出ω,通過函數的最大值,求出x的值,然后確定k的值.利用函數圖象平移的原則:左加右減,上加下減由函數y=sinx的圖象變換得到函數y=f(x)的圖象.
點評:本題是中檔題,考查三角函數的化簡、公式的應用、周期的求法、最值的應用及函數圖象的變換,還考查發現問題解決問題的能力、計算能力,是常考題型.

 =(
=( cosωx,sinωx),
cosωx,sinωx), =(sinωx,0),其中ω>0,記函數f(x)=(
=(sinωx,0),其中ω>0,記函數f(x)=( +
+ )•
)• +k.
+k. ,求ω的取值范圍;
,求ω的取值范圍; ,
, ]時,函數f(x)的最大值是
]時,函數f(x)的最大值是 ,求函數f(x)的解析式,并說明如何由函數y=sinx的圖象變換得到函數y=f(x)的圖象.
,求函數f(x)的解析式,并說明如何由函數y=sinx的圖象變換得到函數y=f(x)的圖象. =(
=( cosωx,sinωx),
cosωx,sinωx), =(sinωx,0),
=(sinωx,0), +
+ =(
=( cosωx+sinωx,sinωx).
cosωx+sinωx,sinωx). +
+ )•
)• +k=
+k= sinωxcosωx+sin2ωx+k
sinωxcosωx+sin2ωx+k sin2ωx+
sin2ωx+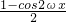 +k=
+k= sin2ωx-
sin2ωx- cos2ωx+
cos2ωx+ +k
+k )+k+
)+k+ .
. =
=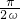 ≥
≥ ,∴ω≤1.
,∴ω≤1. =π,∴ω=1.
=π,∴ω=1. )+k+
)+k+ .
. ,
, ],∴2x-
],∴2x- ∈[-
∈[- ,
, ].
]. =
= ,即x=
,即x= 時,f(x)max=f(
時,f(x)max=f( )=sin
)=sin +k+
+k+ =k+1=
=k+1= ,
, .故f(x)=sin(2x-
.故f(x)=sin(2x- ).
). 個單位長度,得到函數y=sin(x-
個單位長度,得到函數y=sin(x- )的圖象,再將得到的函數圖象上所有點的橫坐標變為原來的
)的圖象,再將得到的函數圖象上所有點的橫坐標變為原來的 倍(縱坐標不變),得到函數y=sin(2x-
倍(縱坐標不變),得到函數y=sin(2x- )的圖象.
)的圖象. ,得到關系式,求出ω的取值范圍;
,得到關系式,求出ω的取值范圍;
