
已知數列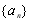 滿足
滿足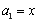 ,
, ,
, ,
,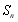 是數列
是數列 的前
的前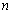 項和.
項和.
(1)若數列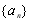 為等差數列.
為等差數列.
①求數列的通項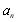 ;
;
②若數列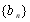 滿足
滿足 ,數列
,數列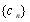 滿足
滿足 ,試比較數列
,試比較數列 前
前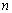 項和
項和 與
與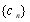 前
前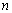 項和
項和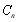 的大小;
的大小;
(2)若對任意 ,
,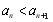 恒成立,求實數
恒成立,求實數 的取值范圍.
的取值范圍.
(1)①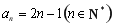
②當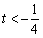 或
或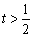 時,
時,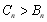 ;當
;當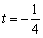 或
或 時,
時,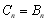 ;當
;當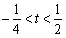 時,
時,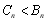
(2)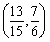
【解析】
試題分析:(1) 解等差數列問題,主要從待定系數對應關系出發.①從 與
與 關系出發,得出
關系出發,得出 ,利用
,利用 解出
解出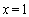 ,從而解出首項與公差,②
,從而解出首項與公差,② 實際是一個等比數列,分別求出數列
實際是一個等比數列,分別求出數列 前
前 項和
項和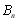 與
與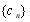 前
前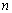 項和
項和 ,要使計算簡便,需用
,要使計算簡便,需用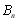 表示
表示 ,比較兩者大小通常用作差法. 作差法的關鍵是因式分解,將差分解為因子,根據因子的符號討論差的正負,從而確定大小,(2) 不等式恒成立問題,首先化簡不等式. 需從
,比較兩者大小通常用作差法. 作差法的關鍵是因式分解,將差分解為因子,根據因子的符號討論差的正負,從而確定大小,(2) 不等式恒成立問題,首先化簡不等式. 需從 與
與 關系出發,得出項的關系:
關系出發,得出項的關系: ,這是三項之間的關系,需繼續化簡成兩項之間關系:
,這是三項之間的關系,需繼續化簡成兩項之間關系: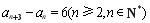 ,這樣原數列分解為三個等差數列,則
,這樣原數列分解為三個等差數列,則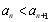 恒成立等價轉化為
恒成立等價轉化為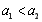 且
且 ,代入可解得
,代入可解得
試題解析:解:(1)因為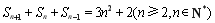 ,所以
,所以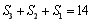 ,
,
即 ,又
,又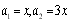 ,所以
,所以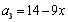 , 2分
, 2分
①又因為數列 成等差數列,所以
成等差數列,所以 ,即
,即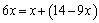 ,解得
,解得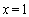 ,
,
所以 ; 4分
; 4分
②因為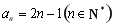 ,所以
,所以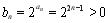 ,其前
,其前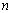 項和
項和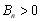 ,
,
又因為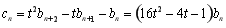 , 5分
, 5分
所以其前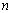 項和
項和 ,所以
,所以 , 7分
, 7分
當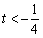 或
或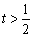 時,
時,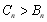 ;當
;當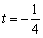 或
或 時,
時,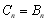 ;
;
當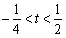 時,
時,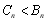 9分
9分
(2)由 知
知 ,
,
兩式作差,得 , 10分
, 10分
所以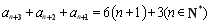 ,作差得
,作差得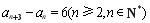 , 11分
, 11分
所以,當 時,
時, ;
;
當 時,
時, ;
;
當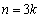 時,
時,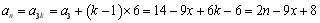 ;
;
當 時,
時, ; 14分
; 14分
因為對任意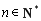 ,
,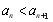 恒成立,所以
恒成立,所以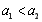 且
且 ,
,
所以 ,解得,
,解得, ,故實數
,故實數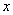 的取值范圍為
的取值范圍為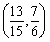 . 16分
. 16分
考點:等差數列通項,等比數列求和,不等式恒成立


 暑假接力賽新疆青少年出版社系列答案
暑假接力賽新疆青少年出版社系列答案科目:高中數學 來源:2013-2014學年江蘇蘇北四市高三第一次質量檢測理科數學試卷(解析版) 題型:解答題
已知數列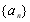 滿足
滿足 ,
,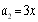 ,
,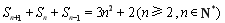 ,
,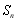 是數列
是數列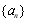 的前
的前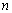 項和.
項和.
(1)若數列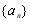 為等差數列.
為等差數列.
(ⅰ)求數列的通項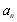 ;
;
(ⅱ)若數列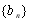 滿足
滿足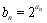 ,數列
,數列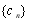 滿足
滿足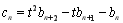 ,試比較數列
,試比較數列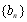 前
前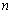 項和
項和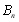 與
與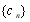 前
前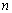 項和
項和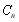 的大小;
的大小;
(2)若對任意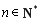 ,
,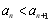 恒成立,求實數
恒成立,求實數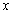 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源:2013-2014學年江蘇蘇北四市高三第一次質量檢測文科數學試卷(解析版) 題型:解答題
已知數列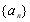 滿足
滿足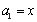 ,
,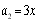 ,
,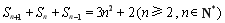 ,
,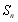 是數列
是數列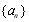 的前
的前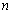 項和.
項和.
(1)若數列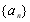 為等差數列.
為等差數列.
(ⅰ)求數列的通項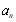 ;
;
(ⅱ)若數列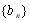 滿足
滿足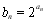 ,數列
,數列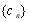 滿足
滿足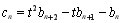 ,試比較數列
,試比較數列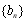 前
前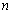 項和
項和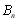 與
與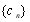 前
前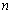 項和
項和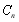 的大小;
的大小;
(2)若對任意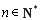 ,
,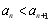 恒成立,求實數
恒成立,求實數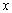 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源:2010-2011年黑龍江省高一下學期期中考試理科數學 題型:選擇題
已知數列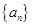 滿足
滿足 ,
,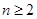 ,點
,點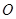 是平面上不在
是平面上不在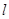 上的任意一點,
上的任意一點,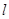 上有不重合的三點
上有不重合的三點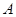 、
、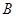 、
、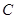 ,又知
,又知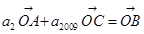 ,則
,則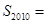
A.1004 B.2010 C.2009 D.1005 ( )
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com