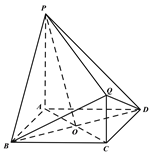
【題目】如圖， 
都與正方形
所在平面垂直， 
， 
（Ⅰ）求證： 
⊥平面
;
（Ⅱ）過點
與平面
平行的平面交
于點
，求
的值.
【答案】（1）見解析（2）
【解析】試題分析:（1）由條件得三角形PAD為等腰三角形,再根據等腰三角形性質得
.計算由勾股定理得
,最后根據線面垂直判定定理得
⊥平面
;（2）設點
與平面
平行的平面交
于點
，由面面平行性質定理得
,所以
試題解析：（Ⅰ）連接
，由題知
,
共面, 
，
∴
,
∴
.
由題中數據得
∴
∽
∴
,
又∵
∴
∴
（或計算
，由勾股定理得出
）
∵
，
∴
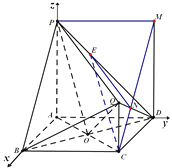
（Ⅱ）如圖，以
為原點，分別以
所在直線為
軸建立直角坐標系，
∴各點坐標分別為
,
∴
=
, 
=
,設平面
的法向量
∴
，得
，
不妨設
，∴
設
,∴
,
，
∵
平面
,∴
與平面
的法向量
垂直。
,
∴
. ∴
（方法二）在平面
中，分別過
點、
點作直線
的平行線相交于點
，
連結
交直線
與點
，在平面
中過點
作直線
交
于點
，
由題可知
∴
,
∴
∵
，
∴
∵
, ∴
科目：高中數學 來源： 題型：
【題目】在平面直角坐標系中，O為坐標原點，已知向量 
=（﹣1，2），又點A（8，0），B（n，t），C（ksinθ，t），θ∈R．
（1）若 
⊥ ，且 
，求向量 
；
（2）若向量 
與向量 共線，常數k＞0，求f（θ）=tsinθ的值域．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數f（x）=lg（2+x），g（x）=lg（2﹣x），設h（x）=f（x）+g（x）
（1）求函數h（x）的定義域．
（2）判斷函數h（x）的奇偶性，并說明理由．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】（Ⅰ）設z=1+i（i是虛數單位），求 
+z2的值； （Ⅱ）設x，y∈R，復數z=x+yi，且滿足|z|2+（z+ 
）i= 
，試求x，y的值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】給出下列命題：
①函數f（x）=loga（2x﹣1）﹣1的圖象過定點（1，0）；
②已知函數f（x）是定義在R上的偶函數，當x≤0時，f（x）=x（x+1），則f（x）的解析式為f（x）=x2﹣|x|；
③若 
，則a的取值范圍是 
；
其中所有正確命題的序號是
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數f（x）=exsinx，其中x∈R，e=2.71828…為自然對數的底數． （Ⅰ）求函數f（x）的單調區間；
（Ⅱ）當 
時，f（x）≥kx，求實數k的取值范圍．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】設函數f（x）=ax2－lnx。
（Ⅰ）當a=
時，判斷f（x）的單調性；（Ⅱ）設f（x）≤x3+4x－lnx，在定義域內恒成立，求a的取值范圍。
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】設f（x）=x3+ax2+bx+1的導函數f′（x）滿足f′（x）=2a，f′（2）=﹣b，
（1）求曲線y=f（x）在點（1，f（1））處的切線方程；
（2）設g（x）=f′（x）ex ， 求函數g（x）的單調區間．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
