已知函數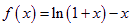 ,數列
,數列 滿足:
滿足:
 .
.
(Ⅰ)求證: ;
;
(Ⅱ)求數列 的通項公式;
的通項公式;
(Ⅲ)求證不等式: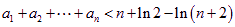
如下
解析:
(Ⅰ)
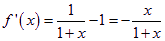
當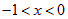 時,
時, ,即
,即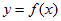 是單調遞增函數;
是單調遞增函數;
當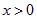 時,
時,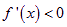 ,即
,即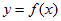 是單調遞減函數;
是單調遞減函數;
所以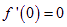 ,即
,即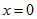 是極大值點,也是最大值點
是極大值點,也是最大值點
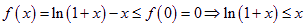 ,當
,當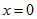 時取到等號. 5分
時取到等號. 5分
(Ⅱ)由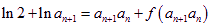 得
得
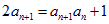
方法1 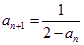
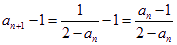

即數列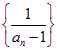 是等差數列,首項為
是等差數列,首項為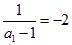 ,公差為
,公差為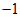
∴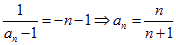
方法2利用函數不動點
方法3利用觀察、歸納、猜想、數學歸納法證明
(Ⅲ)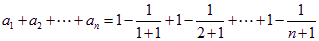
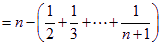
又∵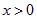 時,有
時,有
令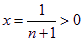 ,則
,則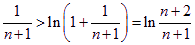
∴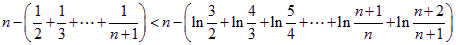
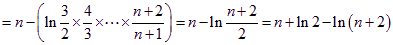
∴
練習冊系列答案
相關習題
科目:高中數學
來源:2011屆河北省石家莊市自強中學高三數學練習試卷5
題型:單選題
查看答案和解析>>
科目:高中數學
來源:2011-2012學年湖北省高三高考模擬理科數學試卷一
題型:解答題
查看答案和解析>>
科目:高中數學
來源:2011-2012學年安徽省東至縣高三一模文科數學試卷
題型:解答題
已知函數 ,數列
,數列 滿足
滿足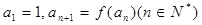
(1)證明 求數列
求數列 的通項公式;
的通項公式;
(2)記 ,求
,求 .
.
查看答案和解析>>
科目:高中數學
來源:河北省三河一中2011-2012學年高三上學期第二次月考(數學文)
題型:解答題
已知函數 ,數列
,數列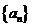 滿足
滿足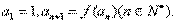
(1)求數列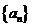 的通項公式;(2)記
的通項公式;(2)記 ,求
,求 .
.
查看答案和解析>>
科目:高中數學
來源:河北省三河一中2011-2012學年高三上學期第二次月考(數學理)
題型:解答題
已知函數 ,數列
,數列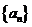 滿足
滿足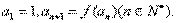
(1)求數列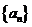 的通項公式;(2)記
的通項公式;(2)記 ,求
,求 .
.
查看答案和解析>>

![]() ,數列
,數列![]() 滿足:
滿足:![]() .
.![]() ;
;![]() 的通項公式;
的通項公式;![]()