Question

【題目】從某企業生產的某種產品中抽取件，測量這些產品的一項質量指標值，由測量結果得如頻率分布直方圖：

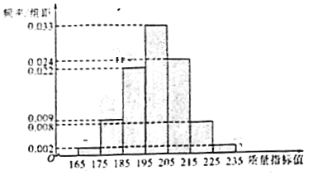
（1）求這件產品質量指標值的樣本平均數和樣本方差（同一組中的數據用該組區間的中點值作代表）；

（2）由直方圖可以認為，這種產品的質量指標值服從正態分布，其中近似為樣本平均數，近似為樣本方差.

①利用該正態分布，求；

②某用戶從該企業購買了件這種產品，記表示這件產品中質量指標值位于區間的產品件數.利用①的結果，求.

附：.若，則，.

Answer 1

【答案】（1），；（2）68.26

【解析】試題分析：（Ⅰ）運用離散型隨機變量的期望和方差公式，即可求出；（Ⅱ）（i）由（Ⅰ）知Z～N（200，150），從而求出P（187．8＜Z＜212．2），注意運用所給數據；（ii）由（i）知X～B（100，0．6826），運用EX=np即可求得

試題解析：（1）抽取產品的質量指標值的樣本平均數和樣本方差s2分別為

＝170×0．02＋180×0．09＋190×0．22＋200×0．33＋210×0．24＋220×0．08＋230×0．02＝200．

s2＝（－30）2×0．02＋（－20）2×0．09＋（－10）2×0．22＋0×0．33＋102×0．24＋202×0．08＋302×0．02＝150．…6分

（2）（i）由（1）知，Z～N（200，150），

從而P（187．8＜Z＜212．2）＝P（200－12．2＜Z＜200＋12．2）＝0．682 6．

（ii）由（i）知，一件產品的質量指標值位于區間（187．8，212．2）的概率為0．682 6，

依題意知X～B（100，0．682 6），

所以EX＝100×0．682 6＝68．26．