
 ,知bn=3×2n-1-2.
,知bn=3×2n-1-2. ,(7分)
,(7分) ,且不討論n=1,扣1分)(10分)
,且不討論n=1,扣1分)(10分)

 提分百分百檢測卷單元期末測試卷系列答案
提分百分百檢測卷單元期末測試卷系列答案 小學期末標準試卷系列答案
小學期末標準試卷系列答案科目:高中數學 來源: 題型:
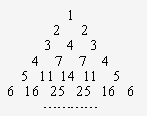
 我們用部分自然數構造如下的數表:用aij(i≥j)表示第i行第j個數(i、j為正整數),使ai1=aii=i;每行中的其余各數分別等于其“肩膀”上的兩個數之和(第一、二行除外,如圖),設第n(n為正整數)行中各數之和為bn.
我們用部分自然數構造如下的數表:用aij(i≥j)表示第i行第j個數(i、j為正整數),使ai1=aii=i;每行中的其余各數分別等于其“肩膀”上的兩個數之和(第一、二行除外,如圖),設第n(n為正整數)行中各數之和為bn.查看答案和解析>>
科目:高中數學 來源: 題型:
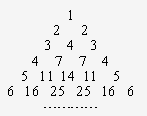
(08年靜安區質檢文)我們用部分自然數構造如下的數表:用![]() 表示第
表示第![]() 行第
行第![]() 個數(
個數(![]() 為正整數),使
為正整數),使![]() ;每行中的其余各數分別等于其“肩膀”上的兩個數之和(第一、二行除外,如圖),設第
;每行中的其余各數分別等于其“肩膀”上的兩個數之和(第一、二行除外,如圖),設第![]() (
(![]() 為正整數)行中各數之和為
為正整數)行中各數之和為![]() .
.
(1)試寫出![]() ,并推測
,并推測![]() 和
和![]() 的關系(無需證明);
的關系(無需證明);
(2)證明數列![]() 是等比數列,并求數列
是等比數列,并求數列![]() 的通項公式
的通項公式![]() ;
;
(3)數列![]() 中是否存在不同的三項
中是否存在不同的三項![]() (
(![]() 為正整數)恰好成等差數列?若存在,求出
為正整數)恰好成等差數列?若存在,求出![]() 的關系;若不存在,請說明理由.
的關系;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
(09年萊陽一中期末文)(12分)
我們用部分自然數構造如下的數表:用![]()
![]() 表示第
表示第![]() 行第
行第![]() 個數為整數
個數為整數![]() ,使
,使![]() ;每行中的其余各數分別等于其‘肩膀”上的兩個數之和(第一、二行除外,如圖),設第
;每行中的其余各數分別等于其‘肩膀”上的兩個數之和(第一、二行除外,如圖),設第![]() (
(![]() 為正整數)行中各數之和為
為正整數)行中各數之和為![]() 。
。

(1) 試寫出![]() 并推測
并推測![]() 和
和![]() 的關系(無需證明);
的關系(無需證明);
(2) 證明數列![]() 是等比數列,并求數列
是等比數列,并求數列![]() 的通項公式
的通項公式![]() ;
;
(3) 數列![]() 中是否存在不同的三項
中是否存在不同的三項![]() 恰好成等差數列?若存在求出
恰好成等差數列?若存在求出![]() 的關系;若不存在,請說明理由。
的關系;若不存在,請說明理由。
查看答案和解析>>
科目:高中數學 來源: 題型:
我們用部分自然數構造如下的數表:用aij(i≥j)表示第i行第j個數(i、j為正整數),使ail=aii=i ;每行中的其余各數分別等于其“肩膀”上的兩個數之和(第一、二行除外,如圖),設第n(n為正整數)行中各數之和為bn.
(1)試寫出b2一2b1;,b3-2b2,b4-2b3,b5-2b4,并推測bn+1和bn的關系(無需證明);
(2)證明數列{bn+2}是等比數列,并求數列{bn}的通項公式bn;
(3)數列{ bn}中是否存在不同的三項bp,bq,br(p,q,r為正整數)恰好成等差數列?若存在求出P,q,r的關系;若不存在,請說明理由.
 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com