
(本小題14分)
(I)已知數列 滿足
滿足
 ,
, 滿足
滿足 ,
,
 ,求證:
,求證: 。.
。.
(II) 已知數列 滿足:a
滿足:a =1且
=1且 。設m
。設m N
N ,m
,m n
n 2,證明(a
2,證明(a +
+ )
) (m-n+1)
(m-n+1)


證明:
(I)記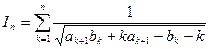 ,則
,則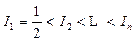 。 …… 2分
。 …… 2分
而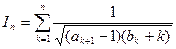
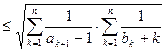 。 ……………… 4分
。 ……………… 4分
因為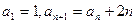 ,所以
,所以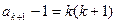 。 ………………… 5分
。 ………………… 5分
從而有 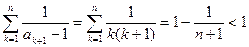 。 ①
。 ①
又因為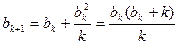 ,所以
,所以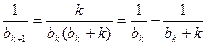 ,
,
即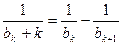 。從而有
。從而有 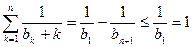 。② … 6分
。② … 6分
由(1)和(2)即得  。綜合得到
。綜合得到 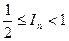 。
。
左邊不等式的等號成立當且僅當 n=1時成立。 ……… 7分
(II)不妨設 即
即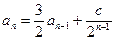 與
與 比較系數得c=1.即
比較系數得c=1.即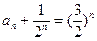

又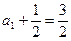 ,故{
,故{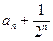 }是首項為
}是首項為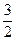 公比為
公比為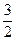 的等比數列,
的等比數列,
故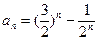 ……… 10分
……… 10分
這一問是數列、二項式定理及不等式證明的綜合問題.綜合性較強.
即證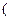
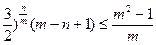 ,當m=n時顯然成立。易驗證當且僅當m=n=2時,等號成立。
,當m=n時顯然成立。易驗證當且僅當m=n=2時,等號成立。
設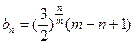 下面先研究其單調性。當
下面先研究其單調性。當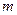 >n時,
>n時,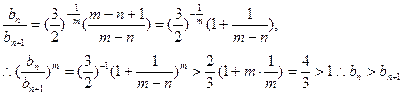 ……… 12分
……… 12分
即數列{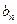 }是遞減數列.因為n
}是遞減數列.因為n 2,故只須證
2,故只須證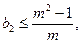 即證
即證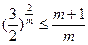 。事實上,
。事實上,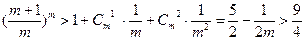 故上不等式成立。綜上,原不等式成立。 ……………… 14分
故上不等式成立。綜上,原不等式成立。 ……………… 14分
解析


科目:高中數學 來源:2010-2011年海南省嘉積中學高二下學期質量檢測數學理卷(一) 題型:填空題
((本小題14分)
已知函數
(I)若函數 在
在 時取得極值,求實數
時取得極值,求實數 的值;
的值;
(II)試討論函數 的單調性;
的單調性;
查看答案和解析>>
科目:高中數學 來源:2014屆福建省高二上學期期中考試文科數學試題(解析版) 題型:解答題
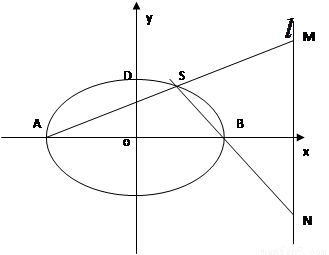
(本小題14分)已知直線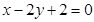 經過橢圓
經過橢圓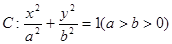 的左頂點A和上頂點D,橢圓
的左頂點A和上頂點D,橢圓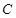 的右頂點為
的右頂點為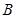 ,點
,點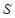 是橢圓
是橢圓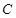 上位于
上位于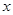 軸上方的動點,直線
軸上方的動點,直線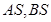 與直線
與直線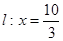 分別交于
分別交于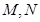 兩點。
兩點。
(I)求橢圓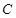 的方程;
的方程;
(Ⅱ)求線段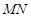 的長度的最小值;
的長度的最小值;
(Ⅲ)當線段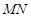 的長度最小時,在橢圓
的長度最小時,在橢圓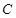 上是否存在這樣的點
上是否存在這樣的點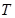 ,使得
,使得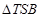 的面積為
的面積為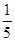 ?若存在,確定點
?若存在,確定點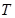 的個數,若不存在,說明理由。
的個數,若不存在,說明理由。
查看答案和解析>>
科目:高中數學 來源:2010-2011年海南省高二下學期質量檢測數學理卷(一) 題型:填空題
((本小題14分)
已知函數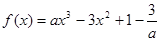
(I)若函數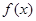 在
在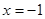 時取得極值,求實數
時取得極值,求實數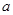 的值;
的值;
(II)試討論函數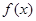 的單調性;
的單調性;

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com