
【題目】已知數列{an}滿足![]() ,且
,且![]() .
.
(1)求證:數列![]() 是等差數列,并求出數列
是等差數列,并求出數列![]() 的通項公式;
的通項公式;
(2)求數列![]() 的前
的前![]() 項和
項和![]() .
.
【答案】(1) an=(2n-1)2n-1;(2) Sn=(2n-3)2n+3.
【解析】
(1)根據等差數列的定義,判斷數列![]() 是等差數列,并寫出它的通項公式以及{an}的通項公式;
是等差數列,并寫出它的通項公式以及{an}的通項公式;
(2)根據數列{an}的前n項和定義,利用錯位相減法求出Sn;
(1)證明:因為an=2an-1+2n,所以![]() =
=![]() =
=![]() +1,
+1,
即![]() -
-![]() =1,所以數列
=1,所以數列![]() 是等差數列,且公差d=1,其首項
是等差數列,且公差d=1,其首項![]() =
=![]() ,所以
,所以![]() =
=![]() +(n-1)×1=n-
+(n-1)×1=n-![]() ,解得an=
,解得an=![]() ×2n=(2n-1)2n-1.
×2n=(2n-1)2n-1.
(2)Sn=1×20+3×21+5×22+…+(2n-1)×2n-1,①
2Sn=1×21+3×22+5×23+…+(2n-3)×2n-1+(2n-1)×2n,②
①-②,得-Sn=1×20+2×21+2×22+…+2×2n-1-(2n-1)2n
=1+![]() -(2n-1)2n=(3-2n)2n-3.
-(2n-1)2n=(3-2n)2n-3.
所以Sn=(2n-3)2n+3.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】有下列四個命題:
①若p是q的充分不必要條件,則¬p是¬q的必要不充分條件;
②若命題p:x≥0,x2+1>0,則¬p:x0<0,x02+1≤0;
③在△ABC中,A>B是sinA>sinB的充要條件;
④命題:當1<t<4時方程![]() 1表示焦點在x軸上的橢圓,為真命題.
1表示焦點在x軸上的橢圓,為真命題.
其中真命題的序號是_____.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】甲、乙兩臺機床生產同一型號零件,記生產的零件的尺寸為![]() ,相關行業質檢部門規定:若
,相關行業質檢部門規定:若![]() ,則該零件為優等品;若
,則該零件為優等品;若![]() ,則該零件為中等品;其余零件為次品.現分別從甲、乙機床生產的零件中各隨機抽取50件,經質里檢測得到下表數據:
,則該零件為中等品;其余零件為次品.現分別從甲、乙機床生產的零件中各隨機抽取50件,經質里檢測得到下表數據:
尺寸 |
|
|
|
|
|
|
甲機床零件頻數 | 2 | 3 | 20 | 20 | 4 | 1 |
乙機床零件頻數 | 3 | 5 | 17 | 13 | 8 | 4 |
(Ⅰ)設生產每件產品的利潤為:優等品3元,中等品1元,次品虧本1元.若將頻率視為概率,試估算甲機床生產一件零件的利潤的數學期望;
(Ⅱ)根據已知條件完成下面的列聯表,并據此數據回答:是否有![]() 的把握認為“零件優等與否和所用機床有關”?
的把握認為“零件優等與否和所用機床有關”?
甲機床 | 乙機床 | 合計 | |
優等品 | |||
非優等品 | |||
合計 |
查看答案和解析>>
科目:高中數學 來源: 題型:
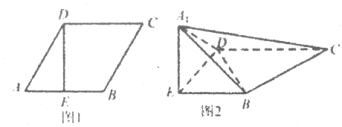
【題目】如圖l,在邊長為2的菱形![]() 中,
中,![]() ,
,![]() 于點
于點![]() ,將
,將![]() 沿
沿![]() 折起到
折起到![]() 的位置,使
的位置,使![]() ,如圖2.
,如圖2.
(1)求證:![]() 平面
平面![]() ;
;
(2)求二面角![]() 的余弦值;
的余弦值;
(3)在線段![]() 上是否存在點
上是否存在點![]() ,使平面
,使平面![]() 平面
平面![]() ?若存在,求
?若存在,求![]() 的值;若不存在,說明理由.
的值;若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 經過點
經過點![]() 離心率
離心率![]() .
.
(Ⅰ)求橢圓的方程;
(Ⅱ)經過橢圓左焦點![]() 的直線(不經過點
的直線(不經過點![]() 且不與
且不與![]() 軸重合)與橢圓交于
軸重合)與橢圓交于![]() 兩點,與直線
兩點,與直線![]() :
:![]() 交于點
交于點![]() ,記直線
,記直線![]() 的斜率分別為
的斜率分別為![]() .則是否存在常數
.則是否存在常數![]() ,使得向量
,使得向量![]()
![]() 共線?若存在求出
共線?若存在求出![]() 的值;若不存在,說明理由.
的值;若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為弘揚民族古典文化,市電視臺舉行古詩詞知識競賽,某輪比賽由節目主持人隨機從題庫中抽取題目讓選手搶答,回答正確將給該選手記正10分,否則記負10分.根據以往統計,某參賽選手能答對每一個問題的概率均為![]() ;現記“該選手在回答完
;現記“該選手在回答完![]() 個問題后的總得分為
個問題后的總得分為![]() ”.
”.
(1)求![]() 且
且![]() (
(![]() )的概率;
)的概率;
(2)記![]() ,求
,求![]() 的分布列,并計算數學期望
的分布列,并計算數學期望![]() .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com