
【題目】設函數f(x)=a﹣ ![]() (a∈R).
(a∈R).
(1)請你確定a的值,使f(x)為奇函數;
(2)用單調性定義證明,無論a為何值,f(x)為增函數.
【答案】
(1)解:∵函數f(x)是R上的奇函數,
∴f(0)=a﹣ ![]() =0,
=0,
∴a=1;
(2)解:證明:任取:x1<x2∈R,
∴f(x1)﹣f(x2)=a﹣ ![]() ﹣a+
﹣a+ ![]() =2
=2 ![]()
∵x1<x2,
∴ ![]() ,
,
又 ![]() >0,
>0, ![]() ,
,
∴f(x1)﹣f(x2)<0,
即f(x1)<f(x2),
∴f(x)在R上的單調遞增
【解析】(1)根據函數奇偶性的定義進行判斷即可.(2)根函數單調性的定義進行證明即可.
【考點精析】掌握函數單調性的判斷方法和函數的奇偶性是解答本題的根本,需要知道單調性的判定法:①設x1,x2是所研究區間內任兩個自變量,且x1<x2;②判定f(x1)與f(x2)的大小;③作差比較或作商比較;偶函數的圖象關于y軸對稱;奇函數的圖象關于原點對稱.


 名校課堂系列答案
名校課堂系列答案科目:高中數學 來源: 題型:
【題目】已知函數![]() 的最小正周期為
的最小正周期為![]() .
.
(1)求函數![]() 的單調增區間;
的單調增區間;
(2)將函數![]() 的圖象向左平移
的圖象向左平移![]() 個單位,再向上平移1個單位,得到函數
個單位,再向上平移1個單位,得到函數![]() 的圖象,若
的圖象,若![]() 在
在![]() 上至少含有10個零點,求
上至少含有10個零點,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】若在曲線f(x,y)=0(或y=f(x))上兩個不同點處的切線重合,則稱這條切線為曲線f(x,y)=0或y=f(x)的“自公切線”.下列方程:
①x2﹣y2=1;
②y=x2﹣|x|;
③y=3sinx+4cosx;
④|x|+1= ![]()
對應的曲線中存在“自公切線”的有( )
A.①③
B.①④
C.②③
D.②④
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知f(x)= ![]() x3﹣x2+ax+m,其中a>0,如果存在實數t,使f′(t)<0,則f′(t+2)f′(
x3﹣x2+ax+m,其中a>0,如果存在實數t,使f′(t)<0,則f′(t+2)f′( ![]() )的值( )
)的值( )
A.必為正數
B.必為負數
C.必為非負
D.必為非正
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,已知曲線
中,已知曲線![]() 的參數方程為
的參數方程為![]() (
(![]() ,
, ![]() 為參數).以坐標原點
為參數).以坐標原點![]() 為極點,
為極點, ![]() 軸的正半軸為極軸,取相同的長度單位建立極坐標系,直線
軸的正半軸為極軸,取相同的長度單位建立極坐標系,直線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)當![]() 時,求曲線
時,求曲線![]() 上的點到直線
上的點到直線![]() 的距離的最大值;
的距離的最大值;
(2)若曲線![]() 上的所有點都在直線
上的所有點都在直線![]() 的下方,求實數
的下方,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,四棱錐![]() 中,底面
中,底面![]() 為梯形,
為梯形, ![]() 底面
底面![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.

(1)求證:平面![]()
![]() 平面
平面![]() ;
;
(2)設![]() 為
為![]() 上的一點,滿足
上的一點,滿足![]() ,若直線
,若直線![]() 與平面
與平面![]() 所成角的正切值為
所成角的正切值為![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,已知四棱錐P﹣ABCD的底面是矩形,側面PAB是正三角形,且平面PAB⊥平面ABCD,E是PA的中點,AC與BD的交點為M. 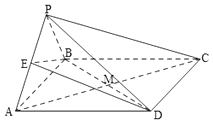
(1)求證:PC∥平面EBD;
(2)求證:BE⊥平面AED.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com