
【題目】已知![]() 是定義在
是定義在![]() 上的奇函數,且
上的奇函數,且![]() .若對任意的
.若對任意的![]() ,
,![]() ,都有
,都有![]() .
.
(1)判斷函數![]() 的單調性,并說明理由;
的單調性,并說明理由;
(2)若![]() ,求實數
,求實數![]() 的取值范圍;.
的取值范圍;.
(3)若不等式![]() 對任意
對任意![]() 和
和![]() 都恒成立,求實數
都恒成立,求實數![]() 的取值范圍.
的取值范圍.
 小學學習好幫手系列答案
小學學習好幫手系列答案 小學同步三練核心密卷系列答案
小學同步三練核心密卷系列答案科目:高中數學 來源: 題型:
【題目】隨著電商的快速發展,快遞業突飛猛進,到目前,中國擁有世界上最大的快遞市場.某快遞公司收取快遞費的標準是:重量不超過![]() 的包裹收費10元;重量超過
的包裹收費10元;重量超過![]() 的包裹,在收費10元的基礎上,每超過
的包裹,在收費10元的基礎上,每超過![]() (不足
(不足![]() ,按
,按![]() 計算)需再收5元.
計算)需再收5元.
該公司將最近承攬的100件包裹的重量統計如下:

公司對近60天,每天攬件數量統計如下表:

以上數據已做近似處理,并將頻率視為概率.
(1)計算該公司未來5天內恰有2天攬件數在101~300之間的概率;
(2)①估計該公司對每件包裹收取的快遞費的平均值;
②根據以往的經驗,公司將快遞費的三分之一作為前臺工作人員的工資和公司利潤,其余的用作其他費用.目前前臺有工作人員3人,每人每天攬件不超過150件,日工資100元.公司正在考慮是否將前臺工作人員裁減1人,試計算裁員前后公司每日利潤的數學期望,若你是決策者,是否裁減工作人員1人?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】以直角坐標系的原點O為極點,x軸的正半軸為極軸建立極坐標系,已知點P的直角坐標為(1,2),點M的極坐標為 ![]() ,若直線l過點P,且傾斜角為
,若直線l過點P,且傾斜角為 ![]() ,圓C以M為圓心,3為半徑.
,圓C以M為圓心,3為半徑.
(1)求直線l的參數方程和圓C的極坐標方程;
(2)設直線l與圓C相交于A,B兩點,求|PA||PB|.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】橢圓![]() 的離心率
的離心率![]() .
.
(1)求橢圓![]() 的方程;
的方程;
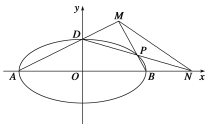
(2)如圖所示,A、B、D是橢圓C的頂點,P是橢圓C上除頂點外的任意一點,直線DP交x軸于點N,直線AD交BP于點M,設BP的斜率為k,MN的斜率為m.證明:2m-k為定值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖![]() 是某公共汽車線路收支差額
是某公共汽車線路收支差額![]() 元與乘客量
元與乘客量![]() 的圖象.由于目前本條線路虧損,公司有關人員提出了兩種扭虧為贏的方案,根據圖
的圖象.由于目前本條線路虧損,公司有關人員提出了兩種扭虧為贏的方案,根據圖![]() 上點
上點![]() 、點
、點![]() 以及射線
以及射線![]() 上的點的實際意義,用文字說明圖
上的點的實際意義,用文字說明圖![]() 方案是______,圖
方案是______,圖![]() 方案是______.
方案是______.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知定義在R上的函數f(x)滿足f(﹣x)=f(x),且當x<0,f(x)=3x+1,若a= ![]() ,b=
,b= ![]() ,c=2
,c=2 ![]() ,則有( )
,則有( )
A.f(a)<f(b)<f(c)
B.f(b)<f(c)<f(a)
C.f(b)<f(a)<f(c)
D.f(c)<f(a)<f(b)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com