Question

設(shè)函數(shù)f（x）=ax²+blnx，其中ab≠0．
證明：當(dāng)ab＞0時，函數(shù)f（x）沒有極值點；當(dāng)ab＜0時，函數(shù)f（x）有且只有一個極值點，并求出極值．

Answer 1

分析：因為函數(shù)有沒有極值點是由導(dǎo)函數(shù)等于0有沒有根決定的，故轉(zhuǎn)化為證ab＞0時導(dǎo)函數(shù)等于0沒有根；ab＜0時，導(dǎo)函數(shù)有且只有一個根，且在根的兩側(cè)導(dǎo)函數(shù)不同號即可．

解答：證明：因為f（x）=ax²+blnx，ab≠0，所以f（x）的定義域為（0，+∞）．f'（x）=2ax+

b

x

=

2ax2+b

x

．
當(dāng)ab＞0時，如果a＞0，b＞0，f'（x）＞0，f（x）在（0，+∞）上單調(diào)遞增；
如果a＜0，b＜0，f'（x）＜0，f（x）在（0，+∞）上單調(diào)遞減．
所以當(dāng)ab＞0，函數(shù)f（x）沒有極值點．
當(dāng)ab＜0時，f′(x)=

2a(x+ - b 2a )(x- - b 2a )

x

令f'（x）=0，
得x1=-

- b 2a

∉(0，+∞)（舍去），x2=

- b 2a

∈(0，+∞)，
當(dāng)a＞0，b＜0時，f'（x），f（x）隨x的變化情況如下表：

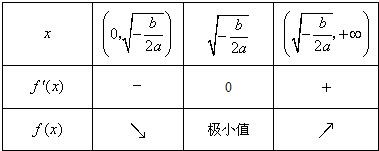
從上表可看出，
函數(shù)f（x）有且只有一個極小值點，極小值為f(

- b 2a

)=-

b

2

[1-ln(-

b

2a

)]．
當(dāng)a＜0，b＞0時，f'（x），f（x）隨x的變化情況如下表：

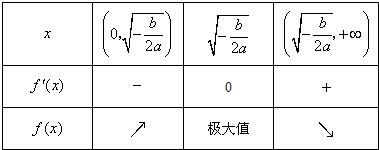
從上表可看出，
函數(shù)f（x）有且只有一個極大值點，極大值為f(

- b 2a

)=-

b

2

[1-ln(-

b

2a

)]．
綜上所述，
當(dāng)ab＞0時，函數(shù)f（x）沒有極值點；
當(dāng)ab＜0時，
若a＞0，b＜0時，函數(shù)f（x）有且只有一個極小值點，極小值為-

b

2

[1-ln(-

b

2a

)]．
若a＜0，b＞0時，函數(shù)f（x）有且只有一個極大值點，極大值為-

b

2

[1-ln(-

b

2a

)]．

點評：本題考查利用導(dǎo)函數(shù)來研究函數(shù)的極值以及對分類討論思想的考查．分類討論思想在數(shù)學(xué)中是非常重要的思想之一，所以希望能加強這方面的訓(xùn)練．