設函數f(x)=x2-ax+bln(x+1)(a,b∈R,且a≠2).
(1)當b=1且函數f(x)在其定義域上為增函數時,求a的取值范圍;
(2)若函數f(x)在x=1處取得極值,試用a表示b;
(3)在(2)的條件下,討論函數f(x)的單調性.
解:(1)當b=1時,函數f(x)=x
2-ax+bln(x+1),
其定義域為(-1,+∞).∴
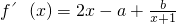
.
∵函數f(x)是增函數,∴當x>-1時,∴
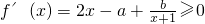
恒成立.
即當x>-1時,
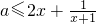
恒成立.
∵當x>-1時,
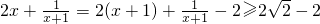
,
且當
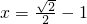
時取等號.∴a的取值范圍為
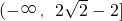
.
(2)∵
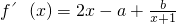
,且函數f(x)在x=1處取得極值,
∴f′(1)=0.∴b=2a-4.此時
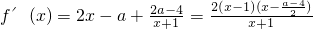
.
當
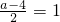
,即a=6時,f'(x)≥0恒成立,
此時x=1不是極值點.∴b=2a-4(a≠6,且a≠2)
(3)由
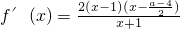
得
①當a<2時,

.∴當-1<x<1時,f′(x)<0;
當x>1時,f′(x)>0.∴當a<2時,
f(x)的單調遞減區間為(-1,1),單調遞增區間為(1,+∞).
②當2<a<6時,
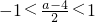
.
∴當-1<x<
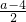
,或x>1時,f'(x)>0;
當
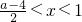
時,f'(x)<0;
∴當2<a<6時,f(x)的單調遞減區間為

,
單調遞增區間為
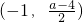
,(1,+∞).
③當a>6時,
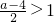
.∴當-1<x<1,或x>
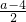
時,f'(x)>0;
當
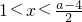
時,f'(x)<0;
∴當a>6時,f(x)的單調遞減區間為
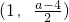
,
單調遞增區間為
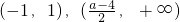
.
綜上所述:∴當a<2時,f(x)的單調遞減區間為(-1,1),
單調遞增區間為(1,+∞);
當2<a<6時,f(x)的單調遞減區間為

,
單調遞增區間為
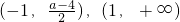
;
當a>6時,f(x)的單調遞減區間為
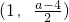
,
單調遞增區間為
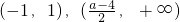
.
分析:(1)當b=1且函數f(x)在其定義域上為增函數,轉化為f′(x)≥0恒成立,x∈(-1,+∞),采取分離參數的方法求得a的取值范圍;(2)若函數f(x)在x=1處取得極值,得f′(1)=0,求出a,b的方程;(3)在(2)的條件下,討論函數f(x)的單調性,求導,比較方程f′(x)=0兩根的大小,確定函數的單調區間.
點評:考查函數在某點取得極值的條件和函數的單調性與導數的關系,在求a的取值范圍時采取的分離參數的方法,轉化為求函數的最值問題,體現了轉化的思想方法,討論函數單調性是,對于程f′(x)=0兩根的大小的比較,體現了分類討論的思想方法,屬難題.

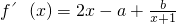 .
.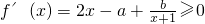 恒成立.
恒成立.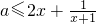 恒成立.
恒成立.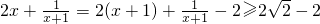 ,
,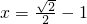 時取等號.∴a的取值范圍為
時取等號.∴a的取值范圍為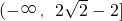 .
.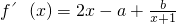 ,且函數f(x)在x=1處取得極值,
,且函數f(x)在x=1處取得極值,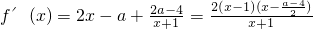 .
.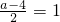 ,即a=6時,f'(x)≥0恒成立,
,即a=6時,f'(x)≥0恒成立,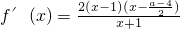 得
得 .∴當-1<x<1時,f′(x)<0;
.∴當-1<x<1時,f′(x)<0;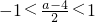 .
.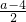 ,或x>1時,f'(x)>0;
,或x>1時,f'(x)>0;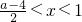 時,f'(x)<0;
時,f'(x)<0; ,
,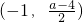 ,(1,+∞).
,(1,+∞).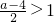 .∴當-1<x<1,或x>
.∴當-1<x<1,或x>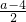 時,f'(x)>0;
時,f'(x)>0;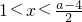 時,f'(x)<0;
時,f'(x)<0;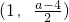 ,
,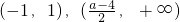 .
. ,
,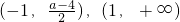 ;
;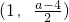 ,
,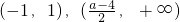 .
.

 尖子生新課堂課時作業系列答案
尖子生新課堂課時作業系列答案 英才計劃同步課時高效訓練系列答案
英才計劃同步課時高效訓練系列答案