
【題目】已知函數![]()
(1)當![]() 時,求曲線y=f(x)在點(1,f(1))處的切線方程;(2)求函數
時,求曲線y=f(x)在點(1,f(1))處的切線方程;(2)求函數![]() 的單調區間和極值
的單調區間和極值
【答案】(1)![]() ;(2)見解析
;(2)見解析
【解析】
(1)把a=1代入原函數解析式中,求出函數在x=1時的導數值,直接利用直線方程的點斜式寫直線方程;
(2)求出函數的導函數,由導函數可知,當a≤0時,f′(x)>0,函數在定義域(0,+∝)上單調遞增,函數無極值,當a>0時,求出導函數的零點,由導函數的零點對定義域分段,利用原函數的單調性得到函數的極值.
(1)當![]() 時
時![]() ,則
,則
![]() ,所以
,所以![]() ,
,
又![]()
所以曲線![]() 在
在![]() 處的切線方程為
處的切線方程為![]() ,
,
即![]()
(2)由![]() 得
得![]() .
.
①當![]() 時,
時,![]() ,函數
,函數![]() 在
在![]() 上單調遞增,函數無極大值,也無極小值;
上單調遞增,函數無極大值,也無極小值;
②當![]() 時,由
時,由![]() 得
得![]() 或
或![]() (舍負),于是當
(舍負),于是當![]() 時、
時、![]() 在
在![]() 上單調遞減;當
上單調遞減;當![]() 時,
時,![]() 在
在![]() 上單調遞增,函數
上單調遞增,函數![]() 在
在![]() 處取得極小值
處取得極小值![]() ,無極大值.
,無極大值.
綜上所述:
當![]() 時,函數
時,函數![]() 的單調遞增區間為
的單調遞增區間為![]() ,函數
,函數![]() 既無極大值也無極小值;
既無極大值也無極小值;
當a>0時,函數![]() 的單調遞減區間是
的單調遞減區間是![]() ,單調遞增區間是
,單調遞增區間是![]() ,函數
,函數![]() 有極小值
有極小值![]() ,無極大值
,無極大值


科目:高中數學 來源: 題型:
【題目】如圖在△AOB中,∠AOB=90°,AO=2,OB=1,△AOC可以通過△AOB以直線AO為軸旋轉得到,且OB⊥OC,點D為斜邊AB的中點.
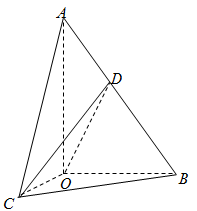
(1)求異面直線OB與CD所成角的余弦值;
(2)求直線OB與平面COD所成角的正弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】《九章算術》中,將底面為長方形且有一條側棱與地面垂直的四棱錐稱之為陽馬,將四個面都為直角三角形的四面體稱之為鱉臑,首屆中國國際進口博覽會的某展館棚頂一角的鋼結構可以抽象為空間圖形陽馬,如圖所示,在陽馬![]() 中,
中,![]() 底面
底面![]() .
.
(1)已知![]() ,斜梁
,斜梁![]() 與底面
與底面![]() 所成角為
所成角為![]() ,求立柱
,求立柱![]() 的長;(精確到
的長;(精確到![]() )
)
(2)求證:四面體![]() 為鱉臑.
為鱉臑.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】化簡
(1)![]()
(2)![]()
【答案】(1) ![]() ;(2)
;(2) ![]() .
.
【解析】試題分析:(1)切化弦可得三角函數式的值為-1
(2)結合三角函數的性質可得三角函數式的值為![]()
試題解析:
(1)tan70°cos10°( ![]() tan20°﹣1)
tan20°﹣1)
=cot20°cos10°( ![]() ﹣1)
﹣1)
=cot20°cos10°(![]() )
)
=![]() ×cos10°×(
×cos10°×(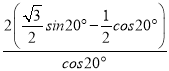 )
)
=![]() ×cos10°×(
×cos10°×(![]() )
)
=![]() ×(﹣
×(﹣![]() )
)
=﹣1
(2)∵(1+tan1°)(1+tan44°)=1+(tan1°+tan44°)+tan1°tan44°
=1+tan(1°+44°)[1﹣tan1°tan44°]+tan1°tan44°=2.
同理可得(1+tan2°)(1+tan43°)
=(1+tan3°)(1+tan42°)
=(1+tan4°)(1+tan41°)=…=2,
故![]() =
=![]()
點睛:三角函數式的化簡要遵循“三看”原則:一看角,這是重要一環,通過看角之間的差別與聯系,把角進行合理的拆分,從而正確使用公式 ;二看函數名稱,看函數名稱之間的差異,從而確定使用的公式,常見的有切化弦;三看結構特征,分析結構特征,可以幫助我們找到變形的方向,如遇到分式要通分等.
【題型】解答題
【結束】
18
【題目】平面內給定三個向量![]()
(1)求![]()
(2)求滿足![]() 的實數
的實數![]() .
.
(3)若![]() ,求實數
,求實數![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某汽車生產廠家為了解某型號電動汽車的“實際平均續航里程數”,收集了使用該型號電動汽車![]() 年以上的部分客戶的相關數據,得到他們的電動汽車的“實際平均續航里程數”.從年齡在40歲以下的客戶中抽取10位歸為A組,從年齡在40歲(含40歲)以上的客戶中抽取10位歸為B組,將他們的電動汽車的“實際平均續航里程數”整理成下圖,其中“+”表示A組的客戶,“⊙”表示B組的客戶.
年以上的部分客戶的相關數據,得到他們的電動汽車的“實際平均續航里程數”.從年齡在40歲以下的客戶中抽取10位歸為A組,從年齡在40歲(含40歲)以上的客戶中抽取10位歸為B組,將他們的電動汽車的“實際平均續航里程數”整理成下圖,其中“+”表示A組的客戶,“⊙”表示B組的客戶.
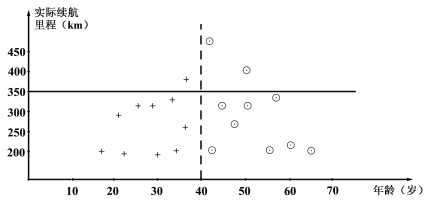
注:“實際平均續航里程數”是指電動汽車的行駛總里程與充電次數的比值.
(Ⅰ)記A,B兩組客戶的電動汽車的“實際平均續航里程數”的平均值分別為![]() ,
,![]() ,根據圖中數據,試比較
,根據圖中數據,試比較![]() ,
,![]() 的大小(結論不要求證明);
的大小(結論不要求證明);
(Ⅱ)從A,B兩組客戶中隨機抽取2位,求其中至少有一位是A組的客戶的概率;
(III)如果客戶的電動汽車的“實際平均續航里程數”不小于350,那么稱該客戶為“駕駛達人”.從A,B兩組客戶中,各隨機抽取1位,記“駕駛達人”的人數為![]() ,求隨機變量
,求隨機變量![]() 的分布列及其數學期望
的分布列及其數學期望![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知數列![]() 中
中![]() ,函數
,函數![]() .
.
(1)若正項數列![]() 滿足
滿足![]() ,試求出
,試求出![]() ,
, ![]() ,
, ![]() ,由此歸納出通項
,由此歸納出通項![]() ,并加以證明;
,并加以證明;
(2)若正項數列![]() 滿足
滿足![]() (n∈N*),數列
(n∈N*),數列![]() 的前項和為Tn,且
的前項和為Tn,且![]() ,求證:
,求證: ![]() .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com