
(2006
福建,18)如下圖,四面體ABCD中,O、E分別是BD、BC的中點,CA=CB=CD=BD=2, .
.
(1)
求證:AO⊥平面BCD;(2)
求異面直線AB與CD所成角的大小;(3)
求點E到平面ACD的距離.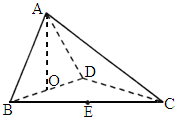
|
解析: (1)連結OC.∵ BO=DO,AB=AD,∴AO⊥BD.∵ BO=DO,BC=CD,∴CO⊥BD.
在△ AOC中,由已知可得AO=1,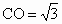 ,而AC=2, ,而AC=2,
∴ 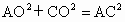 , ,
∴∠ AOC=90°,即AO⊥OC.∵ BD∩OC=O,∴ AO⊥平面BCD.(2) 取AC的中點M,連結OM、ME、OE,由E為BC的中點知ME∥AB,OE∥DC.∴直線 OE與EM所成的銳角就是異面直線AB與CD所成的角.在△ OME中,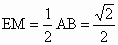 , ,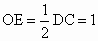 , ,
∵ OM是直角△AOC斜邊上的中線,∴ 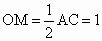 ,∴ ,∴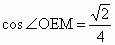 , ,
∴異面直線 AB與CD所成角的大小為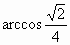 . .
(3) 設點E到平面ACD的距離為h.∵ 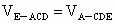 , ,
∴ 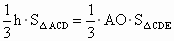 . .
在△ ACD中,CA=CD=2,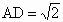 . .
∴ 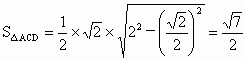 . .
而 AO=1,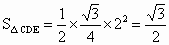 , ,
∴ 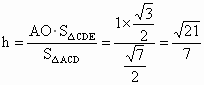 . .
∴點 E到平面ACD的距離為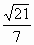 . . |


 教學練新同步練習系列答案
教學練新同步練習系列答案湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com