
(08年莆田四中一模理)(12分)
如圖,在四棱錐![]() 中,底面
中,底面![]() 為矩形,
為矩形,![]() ⊥底面
⊥底面![]() ,
,![]() 是
是![]() 上一點.已知
上一點.已知![]() =
=![]() ,
,![]() ,
,![]() =
=![]()
(1)求證,![]() ⊥平面
⊥平面![]() ;
;
(2)求二面角![]() 的大小.
的大小.

解析:方法一:(1)在Rt△ADE中,AE=AD?tan![]()
![]() -----2分
-----2分
在Rt△ADE和Rt△EBC中,![]()
∴Rt△DAE∽Rt△EBC
∴∠ADE=∠EBC=![]() 又∠AED=
又∠AED=![]()
∴∠DEC=90°即DE⊥EC
又∵PD⊥平面ABCD ∴PD⊥CE
∴CE⊥平面PED --------- 6分
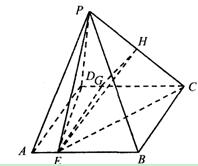
(2)過E作EG⊥CD交CD于G,作GH⊥PC交于PC于H,連結EH.
因PD⊥底面ABCD,所以PD⊥EG. 從而EG⊥平面PCD.
∵GH⊥PC,由三垂線定理得EH⊥PC
∴∠EHG為二面角E―PC―D的平面角 ---------10分
在△PDC中,PD=![]() ,CD=2,GC=
,CD=2,GC=![]()
由△PDC∽△GHC得GH=PD![]() 又EG=AD=
又EG=AD=![]()
∴在Rt△EHG中,GH=EG. ∴∠EHG=![]() ------12分
------12分
方法二:
(1) 以D為原點,![]() 分別為
分別為![]() 軸建立空間直角坐標系,
軸建立空間直角坐標系,
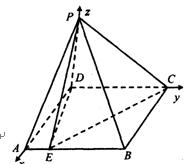
由已知可得
D(0,0,0),P(0,0,![]() ),C(0,2,0),A(
),C(0,2,0),A(![]() ,0,0)
,0,0)
B(![]() --------------2分
--------------2分
![]() -----4分
-----4分
![]() 即CE⊥DE,CE⊥DP ∴CE⊥平面PED (6分)
即CE⊥DE,CE⊥DP ∴CE⊥平面PED (6分)
(2)設平面PEC的法向量n(x,y,z) ------6分
則由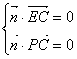 得
得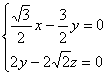
![]() 令
令![]() ,則
,則![]() )--10分
)--10分
∵AD⊥平面PDC ∴![]() 即為平面PDC的法向量
即為平面PDC的法向量

![]() 即二面角E―PC―D的大小為
即二面角E―PC―D的大小為![]() . ----12分
. ----12分


 新課標同步訓練系列答案
新課標同步訓練系列答案 一線名師口算應用題天天練一本全系列答案
一線名師口算應用題天天練一本全系列答案科目:高中數學 來源: 題型:
(08年莆田四中一模理) (14分)
由函數![]() 確定數列
確定數列![]() ,
,![]() ,若函數
,若函數![]() 的反函數
的反函數![]() 能確定數列
能確定數列![]() ,
,![]() ,則稱數列
,則稱數列![]() 是數列
是數列![]() 的“反數列”。
的“反數列”。
(1)若函數![]() 確定數列
確定數列![]() 的反數列為
的反數列為![]() ,求
,求![]() 的通項公式;
的通項公式;
(2)對(1)中![]() ,不等式
,不等式![]() 對任意的正整數
對任意的正整數![]() 恒成立,求實數
恒成立,求實數![]() 的范圍;
的范圍;
(3)設![]() ,若數列
,若數列![]() 的反數列為
的反數列為![]() ,
,![]() 與
與![]() 的公共項組成的數列為
的公共項組成的數列為![]() ;求數列
;求數列![]() 前
前![]() 項和
項和![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
(08年莆田四中一模理)(12分)
某廠生產某種電子元件,如果生產出一件正品,可獲利200元,如果生產出一件次品則損失100元.已
知該廠制造電子元件過程中,次品率![]() 與日產量
與日產量![]() 的函數關系是:
的函數關系是:![]() .
.
(1)將該廠的日盈利額![]() (元)表示為日產量
(元)表示為日產量![]() (件)的函數
(件)的函數![]() ;
;
(2)為獲得最大盈利,該廠的日產量應為多少件?
查看答案和解析>>
科目:高中數學 來源: 題型:
(08年莆田四中一模文)(12分)
已知等差數列![]() }的公差d大于0,且a2、a5是方程x2-12x+27=0的兩根,數列
}的公差d大于0,且a2、a5是方程x2-12x+27=0的兩根,數列![]() }的前n項和為Tn,
}的前n項和為Tn,
且![]()
(I)求數列![]() }、
}、![]() }的通項公式;
}的通項公式;
(II)記![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com