
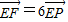 時,求點P到平面ABE的距離.
時,求點P到平面ABE的距離.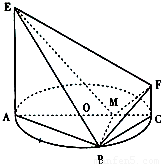
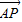 的坐標,利用距離公式可得結論.
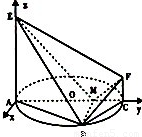
的坐標,利用距離公式可得結論.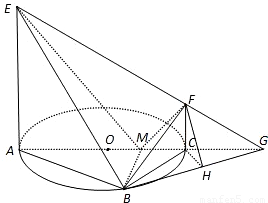 (1)證明:∵EA⊥平面ABC,BM?平面ABC,∴EA⊥BM.
(1)證明:∵EA⊥平面ABC,BM?平面ABC,∴EA⊥BM.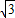 ,BC=2,AM=3,CM=1.∵EA⊥平面ABC,FC∥EA,
,BC=2,AM=3,CM=1.∵EA⊥平面ABC,FC∥EA,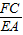 =
=
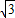 .
.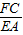 =
=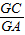 =
= ,得GC=2.∵BG=
,得GC=2.∵BG=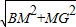 =2
=2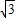 .
.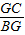 =
=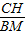 ,則CH=
,則CH=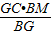 =1.
=1.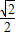 .
.
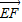 =(0,4,-2)∴
=(0,4,-2)∴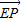 =(0,y,z-3)
=(0,y,z-3)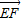 =6
=6 ,∴
,∴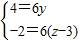 ,∴
,∴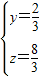
 ,
, ),
),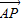 =(0,
=(0, )
)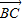 =(
=(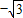 ,1,0)
,1,0)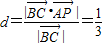 .
.

科目:高中數學 來源: 題型:
 如圖,某城市設立以城中心O為圓心、r公里為半徑的圓形保護區,從保護區邊緣起,在城中心O正東方向上有一條高速公路PB、西南方向上有一條一級公路QC,現要在保護區邊緣PQ弧上選擇一點A作為出口,建一條連接兩條公路且與圓O相切的直道BC.已知通往一級公路的道路AC每公里造價為a萬元,通往高速公路的道路AB每公里造價是m2a萬元,其中a,r,m為常數,設∠POA=θ,總造價為y萬元.
如圖,某城市設立以城中心O為圓心、r公里為半徑的圓形保護區,從保護區邊緣起,在城中心O正東方向上有一條高速公路PB、西南方向上有一條一級公路QC,現要在保護區邊緣PQ弧上選擇一點A作為出口,建一條連接兩條公路且與圓O相切的直道BC.已知通往一級公路的道路AC每公里造價為a萬元,通往高速公路的道路AB每公里造價是m2a萬元,其中a,r,m為常數,設∠POA=θ,總造價為y萬元.
| ||||
| 2 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
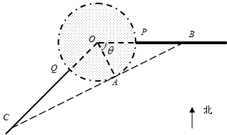 如圖,某城市設立以城中心O為圓心、r公里為半徑的圓形保護區,從保護區邊緣起,在城中心O正東方向上有一條高速公路PB、西南方向上有一條一級公路QC,現要在保護區邊緣PQ弧上選擇一點A作為出口,建一條連接兩條公路且與圓O相切的直道BC.已知通往一級公路的道路AC每公里造價為a萬元,通往高速公路的道路AB每公里造價是m2a萬元,其中a,r,m為常數,設∠POA=θ,總造價為y萬元.
如圖,某城市設立以城中心O為圓心、r公里為半徑的圓形保護區,從保護區邊緣起,在城中心O正東方向上有一條高速公路PB、西南方向上有一條一級公路QC,現要在保護區邊緣PQ弧上選擇一點A作為出口,建一條連接兩條公路且與圓O相切的直道BC.已知通往一級公路的道路AC每公里造價為a萬元,通往高速公路的道路AB每公里造價是m2a萬元,其中a,r,m為常數,設∠POA=θ,總造價為y萬元.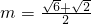 時,如何確定A點的位置才能使得總造價最低?
時,如何確定A點的位置才能使得總造價最低?查看答案和解析>>
科目:高中數學 來源:2012-2013學年江蘇省宿遷市沭陽縣高一(下)期中數學試卷(解析版) 題型:解答題
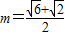 時,如何確定A點的位置才能使得總造價最低?
時,如何確定A點的位置才能使得總造價最低?
查看答案和解析>>
科目:高中數學 來源:陜西省寶雞中學2010屆高三適應性訓練(數學理) 題型:填空題
A.(參數方程與極坐標)
直線 與直線
與直線 的夾角大小為
的夾角大小為
 B.(不等式選講)要使關于x的不等式
B.(不等式選講)要使關于x的不等式 在實數
在實數
范圍內有解,則A的取值范圍是
C.(幾何證明選講) 如圖所示,在圓O中,AB是圓O的直
徑AB =8,E為OB.的中點,CD過點E且垂直于AB,
EF⊥AC,則
CF•CA=
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com